
【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3, 求证:AD平分∠BAC.
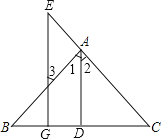
证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°( )
∴∠ADC=∠EGC(等量代换)
∴AD∥EG( )
∴∠1=∠3( )
∠2=∠E( )
又∵∠E=∠3( 已知) ∴∠1=∠2( )
∴AD平分∠BAC( ).
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品8件,B种纪念品3件,需要95元;若购进A种纪念品5件,B种纪念品6件,需要80元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于750元,但不超过764元,那么该商店共有几种进货方案?
(3)已知商家出售一件A种纪念品可获利a元,出售一件B种纪念品可获利(5﹣a)元,试问在(2)的条件下,商家采用哪种方案可获利最多?(商家出售的纪念品均不低于成本价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)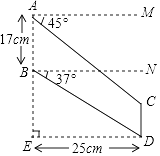
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣2x2﹣1向上平移若干个单位,使抛物线与坐标轴有三个交点,如果这些交点能够成等边三角形,那么平移的距离为( )
A.1个单位
B.![]() 个单位
个单位
C.![]() 个单位
个单位
D.![]() 个单位
个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:
第1个式子: ![]()
第2个式子: ![]()
第3个式子: ![]()
第4个式子: ![]()
![]()
(1)可猜想第7个等式为 .
(2)探索规律,若字母![]() 表示自然数,请写出第
表示自然数,请写出第![]() 个等式 .
个等式 .
(3)试证明你写出的等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(﹣1,0);
⑤当1<x<4时,有y2<y1 ,
其中正确的是( )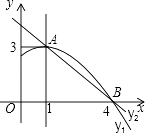
A.①②③
B.①③④
C.①③⑤
D.②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com