
【题目】【探究函数y=x+ ![]() 的图象与性质】
的图象与性质】
(1)函数y=x+ ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下列四个函数图象中函数y=x+ ![]() 的图象大致是;
的图象大致是; 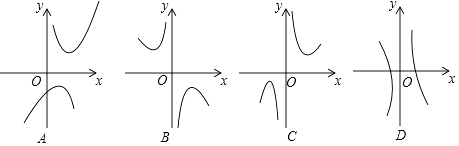
(3)对于函数y=x+ ![]() ,求当x>0时,y的取值范围. 请将下列的求解过程补充完整.
,求当x>0时,y的取值范围. 请将下列的求解过程补充完整.
解:∵x>0
∴y=x+ ![]() =(
=( ![]() )2+(
)2+( ![]() )2=(
)2=( ![]() ﹣
﹣ ![]() )2+
)2+
∵( ![]() ﹣
﹣ ![]() )2≥0
)2≥0
∴y≥ .
(4)若函数y= ![]() ,则y的取值范围 .
,则y的取值范围 .
【答案】
(1)x≠0
(2)C
(3)4;4
(4)y≥13
【解析】解:(1)函数y=x+ ![]() 的自变量x的取值范围是x≠0;(2)函数y=x+
的自变量x的取值范围是x≠0;(2)函数y=x+ ![]() 的图象大致是C;(3)解:∵x>0 ∴y=x+
的图象大致是C;(3)解:∵x>0 ∴y=x+ ![]() =(
=( ![]() )2+(
)2+( ![]() )2=(
)2=( ![]() ﹣
﹣ ![]() )2+4
)2+4
∵( ![]() ﹣
﹣ ![]() )2≥0
)2≥0
∴y≥4.
4)y= ![]() =x+
=x+ ![]() ﹣5═(
﹣5═( ![]() )2+(
)2+( ![]() )2﹣5=(
)2﹣5=( ![]() +
+ ![]() )2+13
)2+13
∵( ![]() ﹣
﹣ ![]() )2≥0,
)2≥0,
∴y≥13.
所以答案是:x≠0,C,4,4,y≥13,
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小,以及对反比例函数的性质的理解,了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() cm,
cm,![]() cm,点
cm,点![]() 为
为![]() 的中点.若点
的中点.若点![]() 在线段
在线段![]() 上以1 cm/s的速度由点
上以1 cm/s的速度由点![]() 向点
向点![]() 运动,到点
运动,到点![]() 时不动.同时,点
时不动.同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.
运动.
(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,经过1 s后,
的运动速度相等,经过1 s后,![]() 与
与![]() 是否全等?请说明理由,并判断此时线段
是否全等?请说明理由,并判断此时线段![]() 和
和![]() 的位置关系;
的位置关系;
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,运动时间为
的运动速度相等,运动时间为![]() s,设
s,设![]() 的面积为
的面积为![]() cm2,请用含
cm2,请用含![]() 的代数式表示
的代数式表示
(3)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
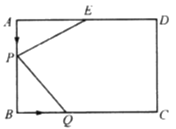
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题9分)把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负性这一性质增加问题的条件,这种解题方法叫做配方法.配方法在代数式求值,解方程,最值问题等都有着广泛的应用.
例如:①用配方法因式分解:a2+6a+8
原式=a2+6a+9-1
=(a+3)2 –1
=(a+3-1)(a+3+1)
=(a+2)(a+4)
②若M=a2-2ab+2b2-2b+2,利用配方法求M的最小值:
a2-2ab+2b2-2b+2=a2-2ab+b2+b2-2b+1+1
=(a-b)2+(b-1)2 +1
∵(a-b)2≥0,(b-1)2 ≥0
∴当a=b=1时,M有最小值1
请根据上述材料解决下列问题:
(1)在横线上添上一个常数项使之成为完全平方式:a 2+4a+ .
(2)用配方法因式分解: a2-24a+143
(3)若M=![]() a2+2a +1,求M的最小值.
a2+2a +1,求M的最小值.
(4)已知a2+b2+c2-ab-3b-4c+7=0,求a+b+c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于 ![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 .
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 . 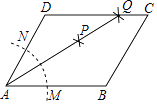
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DBE中,BC=BE,还需要添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )
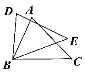
A. AC=DE,∠C=∠E B. BD=AB,AC=DE C. AB=DB,∠A=∠D D. ∠C=∠E,∠A=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com