
【题目】求下列各式的值:
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
(5)![]() +
+![]() (6)
(6) ![]()
【答案】(1)![]() ;(2)-1;(3)
;(2)-1;(3)![]() ;(4)
;(4)![]() ;(5)4;(6)3或-9.
;(5)4;(6)3或-9.
【解析】
(1)先把二次根式化为最简二次根式,然后合并即可;
(2)利用平方差公式计算;
(3)先进行二次根式的乘法运算,然后化简后合并即可;
(4)先把二次根式化为最简二次根式,
(5)先进行二次根式的乘法运算,再利用零指数幂和负整数指数幂的意义计算,然后化简后合并即可;
(6)先把方程变形为(x+3)2=36,然后利用平方根的定义求x.
(1)原式=5![]() +2
+2![]() -6
-6![]()
=![]() ;
;
(2)原式=2-3
=-1;
(3)原式=3![]() -6
-6![]() -3
-3![]()
=-6![]() ;
;
(4)原式=2![]() -
-![]() -
-![]() +3
+3![]()
=![]() ;
;
(5)原式=3+1-3+1+2
=4;
(6)(x+3)2=36,
x+3=±6,
所以x=3或-9.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ![]() ),B(4,0)两点.
),B(4,0)两点. 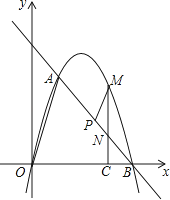
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 ![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.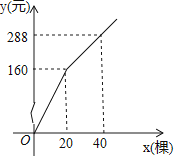
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及平行四边形ABDC的面积![]() .
.
(2)在y轴上是否存在一点P,连接PA,PB,使![]() =2
=2![]() ,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
(3)点P是四边形ABCD边上的点,若△OPC为等腰三角形时,直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→……,白甲壳虫爬行的路线是AB→BB1→……,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2018条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )

A. 0 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知△ABC,以AB、AC为边分别向外作正方形ABFD和正方形ACGE,连结BE、CD,猜想BE与CD有什么数量关系?并说明理由;
(2)请模仿正方形情景下构造全等三角形的思路,利用构造全等三角形完成下题:如图2,要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2﹣6x+c与x轴交于点A(﹣5,0)、B(﹣1,0),与y轴交于点C(0,﹣5),点P是抛物线上的动点,连接PA、PC,PC与x轴交于点D.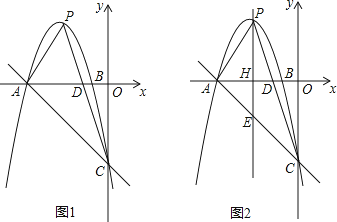
(1)求该抛物线所对应的函数解析式;
(2)若点P的坐标为(﹣2,3),请求出此时△APC的面积;
(3)过点P作y轴的平行线交x轴于点H,交直线AC于点E,如图2.
①若∠APE=∠CPE,求证: ![]() ;
;
②△APE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com