
����Ŀ����ͼ����������ABCD��A1B1C1D1���ⳤΪ1���ڡ��������dz�ͬʱ�ӵ�A����������ͬ���ٶȷֱ�������ǰ���У��ڼdz����е�·����AA1��A1D1���������dz����е�·����AB��BB1�����������Ҷ���ѭ���¹��������еĵ�n��2���n�������ڵ�ֱ�߱����ǼȲ�ƽ��Ҳ���ཻ������n��������������ô���ڡ��������dz���������2018����ֱ�ֹͣ�������������嶥�㴦ʱ������֮��ľ������� ��

A. 0 B. ![]() C.
C. ![]() D. 1
D. 1

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC �У���ACB=90�㣬AC=BC��AE �� BC �ߵ����ߣ�����C �� CF��AE������Ϊ�� F������ B �� BD��BC �� CF ���ӳ����ڵ� D��
��1����֤����AE=CD��
��2���� AC=12cm�����߶� BD �ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������Լ������ƽ��ֱ������ϵ�У�����ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ�ߣ��иõ�ġ������ߡ������磬��M��1��3�����������У�x=1��y=3��y=x+2��y=��x+4��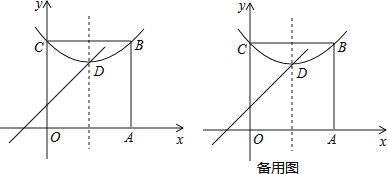
������̽������ͼ����ƽ��ֱ������ϵ����������OABC����B�ڵ�һ���ޣ�A��C�ֱ���x���y���ϣ������� ![]() ����B��C���㣬����D���������ڲ���
����B��C���㣬����D���������ڲ���
��1��ֱ��д����D��m��n�����е������ߣ�
��2������D��һ����������y=x+1����������ߵĽ���ʽ��
��3����P��AB���ϳ���A�������һ�㣬����OP������OAP����OP�۵�����A���ڵ�A���λ�ã�����A����ƽ�����������D�����������ʱ�����㣨2��������������������ƽ�ƶ��پ��룬�䶥������OP�ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ƽ����������ͯ�ڼ��������������ͼ��ʾ��ͼ�е�ĺ�����x��ʾ�Ƽ��ݴ�8��30���ź���ʱ�䣨���ӣ���������y��ʾ����Ƽ��ݵ���������ͼ�����߶�Ӧ�ĺ�������ʽΪy= ![]() ��10��00֮�������οͽ��ٿɺ��Բ��ƣ�
��10��00֮�������οͽ��ٿɺ��Բ��ƣ�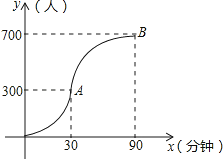
��1����д��ͼ�����߶�Ӧ�ĺ�������ʽ��
��2��Ϊ��֤�Ƽ������ο͵�������������������������684�ˣ����������ڹ�����Ϣ���ȴ�����10��30��ʼ��12��00����½��������ݣ�ƽ��ÿ�������4�ˣ�ֱ�������������ٵ�624��ʱ������ȴ����οͿ�ȫ�����룮���ʹ����ο����ȴ����ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�����Σ�AD��BC����A��90����BC��BD��CE��BD������ΪE��
(1)��֤����ABD�ա�ECB��
(2)����DBC��50��������DCE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ��һ���ı��εĿյ�ABCD����ͼ��ʾ��Ϊ���̻�������ѧУ�ƻ��ڿյ�����ֲ��Ƥ����������A=90�㣬AB=3m��DA=4m��BC=12m��CD=13m��
��1������յ�ABCD�������
��2����ÿ��ֲ1ƽ���ײ�Ƥ��Ҫ200Ԫ�����ܹ���Ͷ�����Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC���ܳ���16��OB��OC�ֱ�ƽ����ABC����ACB��OD��BC��D��OD=2����ABC�������________________.
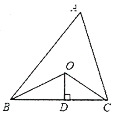
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com