Question

【题目】（1）如图1，已知△ABC，以AB、AC为边分别向外作正方形ABFD和正方形ACGE，连结BE、CD，猜想BE与CD有什么数量关系？并说明理由；

（2）请模仿正方形情景下构造全等三角形的思路，利用构造全等三角形完成下题：如图2，要测量池塘两岸相对的两点B、E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长（结果保留根号）．

Answer 1

【答案】(1)、CD=BE，证明过程见解析；(2)、100.

【解析】

试题分析：(1)、由正方形的性质就可以得出△ADC≌△ABE，就可以得出CD=BE；

(2)、在AB的外侧作AD⊥AB，使AD=AB，连结CD，BD，就可以得出△ADC≌△ABE，就有CD=BE，在Rt△CDB中由勾股定理就可以求出CD的值，进而得出结论．

试题解析：(1)、CD=BE． 理由：如图①∵四边形ABFD和四边形ACGE都是正方形，

∴AD=AB，AC=AE，∠DAB=∠CAE=90°， ∴∠DAB+∠BAC=∠CAE+∠BAC， ∴∠DAC=∠BAE．

在△ADC和△ABE中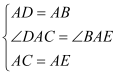， ， ∴△ADC≌△ABE（SAS）， ∴CD=BE；

(2)、如图②，在AB的外侧作AD⊥AB，使AD=AB，连结CD，BD， ∴∠DAB=90°，

∴∠ABD=∠ADB=45°． ∵∠ABC=45°， ∴∠ABD+∠ABC=45°+45°=90°， 即∠DBC=90°．

∴∠CAE=90°， ∴∠DAB=∠CAE， ∴∠DAB+∠BAC=∠CAE+∠BAC， 即∠DAC=∠BAE．

在△ADC和△ABE中 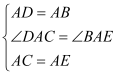， ∴△ADC≌△ABE（SAS）， ∴CD=BE．

∵AB=100m，在直角△ABD中，由勾股定理，得 BD=100． ∴CD==100，

∴BE=CD=100，