
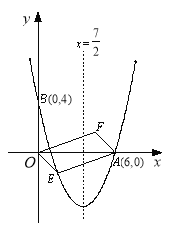
【题目】如图,对称轴为直线x=![]() 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
【答案】(1)由抛物线的对称轴是![]() ,可设解析式为
,可设解析式为![]() .
.
把A、B两点坐标代入上式,得
 解之,得
解之,得![]()
故抛物线解析式为![]() ,顶点为
,顶点为![]()
(2)∵点![]() 在抛物线上,位于第四象限,且坐标适合
在抛物线上,位于第四象限,且坐标适合
![]() ,
,
∴y<0,即 -y>0,-y表示点E到OA的距离.
∵OA是![]() 的对角线,
的对角线,
∴![]() .
.
因为抛物线与![]() 轴的两个交点是(1,0)的(6,0),所以,自变量
轴的两个交点是(1,0)的(6,0),所以,自变量![]() 的
的
取值范围是1<![]() <6.
<6.
根据题意,当S = 24时,即![]() .
.
化简,得![]() 解之,得
解之,得![]()
故所求的点E有两个,分别为E1(3,-4),E2(4,-4).
点E1(3,-4)满足OE = AE,所以![]() 是菱形;
是菱形;
点E2(4,-4)不满足OE = AE,所以![]() 不是菱形.
不是菱形.
当OA⊥EF,且OA = EF时,![]() 是正方形,此时点E的坐标只能是(3,-3).
是正方形,此时点E的坐标只能是(3,-3).
而坐标为(3,-3)的点不在抛物线上,故不存在这样的点E,使![]() 为正方形.
为正方形.
【解析】(1)已知了抛物线的对称轴解析式,可用顶点式二次函数通式来设抛物线,然后将A、B两点坐标代入求解即可.
(2)平行四边形的面积为三角形OEA面积的2倍,因此可根据E点的横坐标,用抛物线的解析式求出
①将S=24代入S,x的函数关系式中求出x的值,即可得出E点的坐标和OE,OA的长;如果平行四边形OEAF是菱形,则需满足平行四边形相邻两边的长相等,据此可判断出四边形OEAF是否为菱形.
②如果四边形OEAF是正方形,那么三角形OEA应该是等腰直角三角形,即E点的坐标为(3,﹣3)将其代入抛物线的解析式中即可判断出是否存在符合条件的E点.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
(1)求A、B之间的路程(保留根号);
(2)已知本路段对校车限速为12米/秒若测得某校车从A到B用了2秒,这辆校车是否超速?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,四块阴影部分的面积分别为S1、S2、S3、S4.则S1+S2+S3+S4等于( )
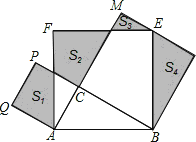
A.14 B.16 C.18 D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】灌云教育局为了解今年九年级学生体育测试情况,随机抽查了部分学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
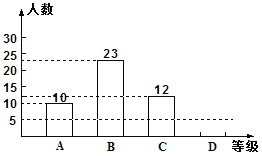
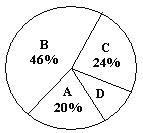
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)样本中D级的学生人数占全班学生人数的百分比是_____________;
(3)扇形统计图中A级所在的扇形的圆心角度数是_____________;
(4)若该县九年级有8000名学生,请你用此样本估计体育测试中A级和B级的学生人数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
我们知道“在数轴上表示的两个数,右边的数总比左边的数大”,利用此规律,我们可以求数轴上两个点之间的距离,具体方法是:用右边的数减去左边的数的差就是表示这两个数的两点之间的距离.若点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 在点
在点![]() 的右边(即
的右边(即![]() ),则点
),则点![]() ,
,![]() 之间的距离为
之间的距离为![]() (即
(即![]() ).
).
例如:若点![]() 表示的数是-6,点
表示的数是-6,点![]() 表示的数是-9,则线段
表示的数是-9,则线段![]() .
.
(理解应用)
(1)已知在数轴上,点![]() 表示的数是-2020,点
表示的数是-2020,点![]() 表示的数是2020,求线段
表示的数是2020,求线段![]() 的长;
的长;
(拓展应用)
如图,数轴上有三个点,点![]() 表示的数是-2,点
表示的数是-2,点![]() 表示的数是3,点
表示的数是3,点![]() 表示的数是
表示的数是![]() .
.
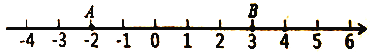
(2)当![]() ,
,![]() ,
,![]() 三个点中,其中一个点是另外两个点所连线段的中点时,求
三个点中,其中一个点是另外两个点所连线段的中点时,求![]() 的值;
的值;
(3)在点![]() 左侧是否存在一点
左侧是否存在一点![]() ,使点
,使点![]() 到点
到点![]() ,点
,点![]() 的距离和为19?若存在,求出点
的距离和为19?若存在,求出点![]() 表示的数:若不存在,请说明理由.
表示的数:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
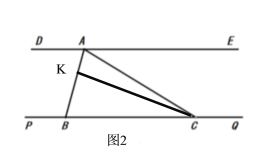
【题目】如图,点![]() 是直角三角形
是直角三角形![]() 斜边
斜边![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() ,分别过点
,分别过点![]() ,
,![]() 向直线
向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 的中点.
的中点.
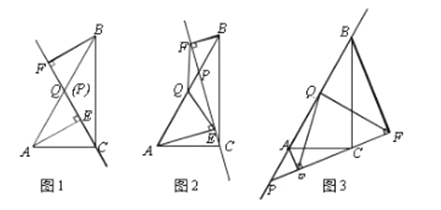
(1)如图1,当点![]() 与点
与点![]() 重合时,
重合时,![]() 与
与![]() 的位置关系是______,
的位置关系是______,![]() 与
与![]() 的数量关系是______;
的数量关系是______;
(2)如图2,当点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 重合)时,试猜想
重合)时,试猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,此时(2)中的结论是否仍成立?请说明理由.
的延长线上时,此时(2)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一直角三角板![]() 的直角顶点
的直角顶点![]() 在直线
在直线![]() 上,作射线
上,作射线![]() 三角板的各边和射线
三角板的各边和射线![]() 都处于直线
都处于直线![]() 的上方.
的上方.
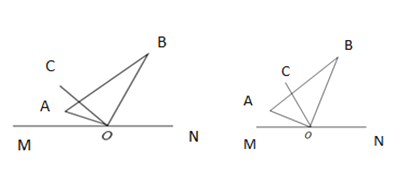
(1)将三角板绕![]() 点在平面内旋转,当
点在平面内旋转,当![]() 平分
平分![]() 时,如图1,如果
时,如图1,如果![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,将三角板![]() 绕
绕![]() 点在平面内任意转动,如果
点在平面内任意转动,如果![]() 始终在
始终在![]() 内,且
内,且![]() ,请问:
,请问:![]() 和
和![]() 有怎样的数量关系?
有怎样的数量关系?
(3)如图2,如果![]() 平分
平分![]() ,
,![]() 是否也平分
是否也平分![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
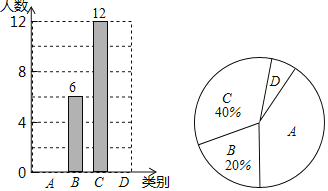
请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 在直线
在直线![]() 上,点
上,点![]() 都在直线
都在直线![]() 上(点
上(点![]() 在点
在点![]() 的左侧),连接
的左侧),连接![]() ,
,![]() 平分
平分![]() 且
且![]()

(1)如图1,求证: ![]()
(2)如图2,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求
,求![]() 的度数
的度数
(3)在(2)的条件下,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的度数(要求:在备用图中画出图形后,再计算)
的度数(要求:在备用图中画出图形后,再计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com