
【题目】随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
(1)求A、B之间的路程(保留根号);
(2)已知本路段对校车限速为12米/秒若测得某校车从A到B用了2秒,这辆校车是否超速?请说明理由.

科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60![]() m的点D(点D与楼底C在同一水平面上)出发,沿斜面坡比为i=1∶
m的点D(点D与楼底C在同一水平面上)出发,沿斜面坡比为i=1∶![]() 的斜坡DB前进30 m到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30 m到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生2018年初中毕业体育学业考试成绩统计表如下:
成绩/分 | 45 | 49 | 52 | 54 | 55 | 58 | 60 |
人数 | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据上表中信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是55分
C.该班学生这次考试成绩的中位数是55分
D.该班学生这次考试成绩的平均数是55分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校进行校园美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,如果由甲队先做20天,剩下的工程由甲、乙合作24天完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需要支付工程款3.5万元,乙队施工一天需要支付工程款2万元:如果规定在70天内完成这项工作,是由甲、乙两队单独完成省钱?还是由甲乙合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金![]() 元,要使(2)中所有方案获利相同,
元,要使(2)中所有方案获利相同,![]() 值应是多少?此时,哪种方案对公司更有利?
值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点![]() 分别表示数
分别表示数![]() ,且
,且![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右运动,点
个单位长度的速度沿数轴向右运动,点![]() 始终为线段
始终为线段![]() 的中点,设点
的中点,设点![]() 运动的时间为
运动的时间为![]() 秒.则:
秒.则:
![]()
![]() 在点
在点![]() 运动过程中,用含
运动过程中,用含![]() 的式子表示点
的式子表示点![]() 在数轴上所表示的数.
在数轴上所表示的数.
![]() 当
当![]() 时,点
时,点![]() 在数轴上对应的数是什么?
在数轴上对应的数是什么?
![]() 设点
设点![]() 始终为线段
始终为线段![]() 的中点,某同学发现,当点
的中点,某同学发现,当点![]() 运动到点
运动到点![]() 右侧时,线段
右侧时,线段![]() 长度始终不变.请你判断该同学的说法是否正确,并加以证明.
长度始终不变.请你判断该同学的说法是否正确,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
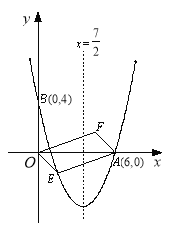
【题目】如图,对称轴为直线x=![]() 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com