
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
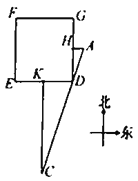
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.
科目:初中数学 来源: 题型:
【题目】一直角三角板![]() 的直角顶点
的直角顶点![]() 在直线
在直线![]() 上,作射线
上,作射线![]() 三角板的各边和射线
三角板的各边和射线![]() 都处于直线
都处于直线![]() 的上方.
的上方.
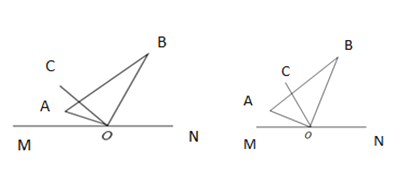
(1)将三角板绕![]() 点在平面内旋转,当
点在平面内旋转,当![]() 平分
平分![]() 时,如图1,如果
时,如图1,如果![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,将三角板![]() 绕
绕![]() 点在平面内任意转动,如果
点在平面内任意转动,如果![]() 始终在
始终在![]() 内,且
内,且![]() ,请问:
,请问:![]() 和
和![]() 有怎样的数量关系?
有怎样的数量关系?
(3)如图2,如果![]() 平分
平分![]() ,
,![]() 是否也平分
是否也平分![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() .下面给出运用反证法证明的四个步骤:①∴
.下面给出运用反证法证明的四个步骤:①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾
矛盾
②因此假设不成立.∴![]()
③假设在![]() 中,
中,![]()
④由![]() ,得
,得![]() ,即
,即![]()
这四个步骤正确的顺序应是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 在直线
在直线![]() 上,点
上,点![]() 都在直线
都在直线![]() 上(点
上(点![]() 在点
在点![]() 的左侧),连接
的左侧),连接![]() ,
,![]() 平分
平分![]() 且
且![]()

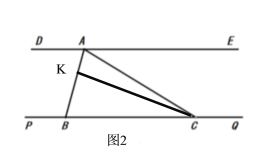
(1)如图1,求证: ![]()
(2)如图2,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求
,求![]() 的度数
的度数
(3)在(2)的条件下,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的度数(要求:在备用图中画出图形后,再计算)
的度数(要求:在备用图中画出图形后,再计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列代数式或方程解应用题:
![]() 已知小明的年龄是
已知小明的年龄是![]() 岁,小红的年龄比小明的年龄的
岁,小红的年龄比小明的年龄的![]() 倍小
倍小![]() 岁,小华的年龄比小红的年龄大
岁,小华的年龄比小红的年龄大![]() 岁,求这三名同学的年龄的和.
岁,求这三名同学的年龄的和.
![]() 小亮与小明从学校同时出发去看在首都体育馆举行的一场足球赛, 小亮每分钟走
小亮与小明从学校同时出发去看在首都体育馆举行的一场足球赛, 小亮每分钟走![]() ,他走到足球场等了
,他走到足球场等了![]() 分钟比赛才开始:小明每分钟走
分钟比赛才开始:小明每分钟走![]() ,他走到足球场,比赛已经开始了
,他走到足球场,比赛已经开始了![]() 分钟.问学校与足球场之间的距离有多远?
分钟.问学校与足球场之间的距离有多远?
![]() 请根据图中提供的信息,回答下列问题:
请根据图中提供的信息,回答下列问题:

①一个水瓶与一个水杯分别是多少元?
②甲、乙两家商场都销售该水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,单独购买的水杯仍按原价销售.若某单位想在一家商场买![]() 个水瓶和
个水瓶和![]() 个水杯,请问选择哪家商场更合算?请说明理由.
个水杯,请问选择哪家商场更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
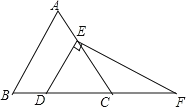
【题目】在等边三角形ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
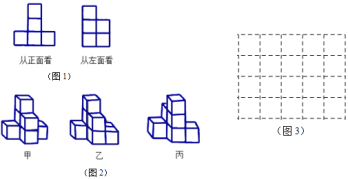
【题目】一个由若干小正方形堆成的几何体,它从正面看和从左面看的图形如图1所示.
![]() 这个几何体可以是图2中甲,乙,丙中的______;
这个几何体可以是图2中甲,乙,丙中的______;
![]() 这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
![]() 请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.

(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com