
【题目】列代数式或方程解应用题:
![]() 已知小明的年龄是
已知小明的年龄是![]() 岁,小红的年龄比小明的年龄的
岁,小红的年龄比小明的年龄的![]() 倍小
倍小![]() 岁,小华的年龄比小红的年龄大
岁,小华的年龄比小红的年龄大![]() 岁,求这三名同学的年龄的和.
岁,求这三名同学的年龄的和.
![]() 小亮与小明从学校同时出发去看在首都体育馆举行的一场足球赛, 小亮每分钟走
小亮与小明从学校同时出发去看在首都体育馆举行的一场足球赛, 小亮每分钟走![]() ,他走到足球场等了
,他走到足球场等了![]() 分钟比赛才开始:小明每分钟走
分钟比赛才开始:小明每分钟走![]() ,他走到足球场,比赛已经开始了
,他走到足球场,比赛已经开始了![]() 分钟.问学校与足球场之间的距离有多远?
分钟.问学校与足球场之间的距离有多远?
![]() 请根据图中提供的信息,回答下列问题:
请根据图中提供的信息,回答下列问题:

①一个水瓶与一个水杯分别是多少元?
②甲、乙两家商场都销售该水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,单独购买的水杯仍按原价销售.若某单位想在一家商场买![]() 个水瓶和
个水瓶和![]() 个水杯,请问选择哪家商场更合算?请说明理由.
个水杯,请问选择哪家商场更合算?请说明理由.
【答案】(1)这三名同学的年龄的和是(5m﹣7)岁;(2)学校离足球场1920m;(3)①一个水瓶40元,一个水杯是8元;②选择乙商场购买更合算.
【解析】
(1)根据题意分别列出小明、小红和小华的年龄,再相加,去括号,合并同类项,即可求出这三名同学的年龄的和;
(2)设学校到足球场xm,根据时间=路程÷速度结合小亮比小明早到8分钟,即可得出关于x的一元一次方程,解之即可得出结论;
(3)①设一个水瓶x元,表示出一个水杯为(48-x)元,根据题意列出方程,求出方程的解即可得到结果;
②计算出两商场得费用,比较即可得到结果.
(1)解:∵小红的年龄比小明的年龄的2倍小4岁,
∴小红的年龄为(2m﹣4)岁.
又∵小华的年龄比小红的年龄的大1岁,
∴小华的年龄为[(2m﹣4)+1](岁),·
∴这三名同学的年龄的和为m+(2m﹣4)+[(2m﹣4)+1]
=m+2m﹣4+2m﹣3
=(5m﹣7)岁.
答:这三名同学的年龄的和是(5m﹣7)岁.
(2)解:设学校到足球场xm,
根据题意得:![]() ﹣
﹣![]() =8,
=8,
解得:x=1920.
答:学校离足球场1920m.
(3)①设一个水瓶x元,表示出一个水杯为(48﹣x)元,
根据题意得:3x+4(48﹣x)=152,
解得:x=40,
则一个水瓶40元,一个水杯是8元;
②甲商场所需费用为(40×5+8×20)×80%=288(元);
乙商场所需费用为5×40+(20﹣5×2)×8=280(元),
∵288>280,
∴选择乙商场购买更合算.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】“五一”期间,小明到小陈家所在的美丽乡村游玩,在村头A处小明接到小陈发来的定位,发现小陈家C在自己的北偏东45°方向,于是沿河边笔直的绿道l步行200米到达B处,这时定位显示小陈家C在自己的北偏东30°方向,如图所示,根据以上信息和下面的对话,请你帮小明算一算他还需沿绿道继续直走多少米才能到达桥头D处(精确到1米)(备用数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进了一批![]() 、
、![]() 两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
类型 | 进购数量(个) | 进价(元/个) | 售价(元/个) |
| 20 | 1800 | 2300 |
| 40 | 1500 | ? |
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元,则![]() 型智能扫地机器人的销售单价至少是多少元?
型智能扫地机器人的销售单价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
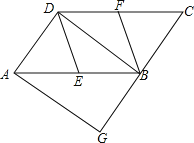
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.
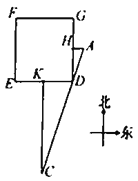
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
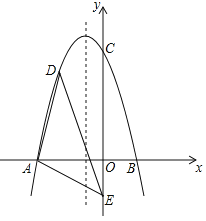
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
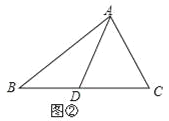
【题目】(1)如图①,AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系?为什么?
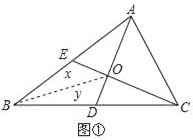
(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC.如图②,已知S△ABC=1.△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.
小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,由(1)结论可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有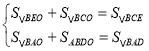 即
即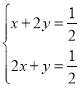 所以x+y=
所以x+y=![]() .即四边形BDOE面积为
.即四边形BDOE面积为![]() .
.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1.D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.
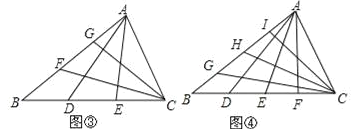
②如图④,已知S△ABC=1.D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC,∠C=90°,AB=10,且cosA=![]() . M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
. M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
⑴ 试说明△AMQ∽△PME;
⑵ 当△PME是等腰三角形时,求出线段AQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com