
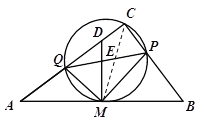
【题目】已知Rt△ABC,∠C=90°,AB=10,且cosA=![]() . M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
. M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
⑴ 试说明△AMQ∽△PME;
⑵ 当△PME是等腰三角形时,求出线段AQ的长.
【答案】(1)证明见解析(2)5或![]()
【解析】(1) 连接MC ,根据直角三角形斜边上的中线等于斜边的一半,得到MC=MA=![]() AB,由同弧所对的圆周角相等推出∠A=∠EPM ,再利用同角的余角相等,即可求解; (2)分三种情况讨论:当AM=AQ时; 当QA=QM时; 当MQ=AM时.
AB,由同弧所对的圆周角相等推出∠A=∠EPM ,再利用同角的余角相等,即可求解; (2)分三种情况讨论:当AM=AQ时; 当QA=QM时; 当MQ=AM时.
⑴ 连接MC,
∵∠C=90°,M是AB中点, ∴MC=MA=![]() ,
,
∴∠A=∠MCA,
∵∠MCA=∠EPM, ∴∠A=∠EPM.
∵PQ为直径 ,
∴∠PMQ=90°.
∴∠PME+∠QME =90°.
∵DM⊥AB,
∴∠AMD=90°.∴∠AMQ +∠QME =90°.
∴∠AMQ=∠PME,
∴△AMQ∽△PME
⑵AB=10,M为线段AB的中点,∴AM=5,AD=![]() =
=![]() =
=![]()
当△AMQ等腰三角形时,△MPE也是等腰三角形.
当AM=AQ时,AQ=5;
当QA=QM时,AQ=![]() ;
;
由题意MQ≠![]() .
.
综上所述,当△MPE是等腰三角形时,线段AQ长为![]() 或
或![]() .
.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】列代数式或方程解应用题:
![]() 已知小明的年龄是
已知小明的年龄是![]() 岁,小红的年龄比小明的年龄的
岁,小红的年龄比小明的年龄的![]() 倍小
倍小![]() 岁,小华的年龄比小红的年龄大
岁,小华的年龄比小红的年龄大![]() 岁,求这三名同学的年龄的和.
岁,求这三名同学的年龄的和.
![]() 小亮与小明从学校同时出发去看在首都体育馆举行的一场足球赛, 小亮每分钟走
小亮与小明从学校同时出发去看在首都体育馆举行的一场足球赛, 小亮每分钟走![]() ,他走到足球场等了
,他走到足球场等了![]() 分钟比赛才开始:小明每分钟走
分钟比赛才开始:小明每分钟走![]() ,他走到足球场,比赛已经开始了
,他走到足球场,比赛已经开始了![]() 分钟.问学校与足球场之间的距离有多远?
分钟.问学校与足球场之间的距离有多远?
![]() 请根据图中提供的信息,回答下列问题:
请根据图中提供的信息,回答下列问题:

①一个水瓶与一个水杯分别是多少元?
②甲、乙两家商场都销售该水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,单独购买的水杯仍按原价销售.若某单位想在一家商场买![]() 个水瓶和
个水瓶和![]() 个水杯,请问选择哪家商场更合算?请说明理由.
个水杯,请问选择哪家商场更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:数轴上任意两点之间的距离与这两点对应的数的关系.
![]()
(1)如果点A表示数5,将点A先向左移动4个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
如果点A表示数﹣2,将点A向右移动5个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
(2)发现:在数轴上,如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为 (用m、n表示,且m≥n).
(3)应用:利用你发现的结论解决下列问题:数轴上表示x和﹣2的两点P与Q之间的距离是3,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
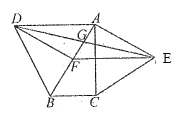
【题目】如图,分别以![]() 的斜边
的斜边![]() ,直角边
,直角边![]() 为边向外作等边
为边向外作等边![]() 和
和![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 相交于点
相交于点![]() .若∠BAC=30°,下列结论:①
.若∠BAC=30°,下列结论:①![]() ;②四边形
;②四边形![]() 为平行四边形;③
为平行四边形;③![]() ;④
;④![]() .其中正确结论的序号是______.
.其中正确结论的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
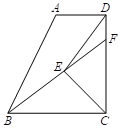
【题目】如图,在四边形ABCD中,∠ADC=∠BCD=90°,BC=CD=2AD,E为∠BCD平分线上的点,连接BE、DE, 延长BE交CD于点F.
⑴ 求证:△BCE≌△DCE;
⑵ 若DE∥AB,求证:FD=FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.

(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
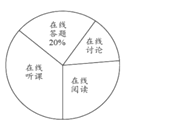
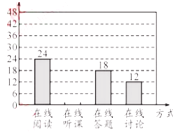
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生![]() 人,请你估计该校对在线阅读最感兴趣的学生人数.
人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
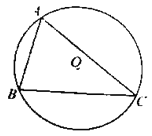
【题目】如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com