
����Ŀ��̽������������������֮��ľ������������Ӧ�����Ĺ�ϵ��
![]()
��1�������A��ʾ��5������A�������ƶ�4����λ���ȵ����B����ô��B��ʾ������������A��B�����ľ��������� ��
�����A��ʾ����2������A�����ƶ�5����λ���ȵ����B����ô��B��ʾ������������A��B�����ľ������� ��
��2�����֣��������ϣ������M��Ӧ������m����N��Ӧ������n����ô��M���N֮��ľ���ɱ�ʾΪ�� ����m��n��ʾ����m��n����
��3��Ӧ���������㷢�ֵĽ��۽���������⣺�����ϱ�ʾx�ͩ�2������P��Q֮��ľ�����3����x=���� ��
���𰸡���1��1�� 4 �� 3�� 5����2��m��n����3��1 ����5.
��������
�������
�����A��ʾ��5����B��ʾ������5-4=1,A��B�����ľ�����5-(1)=4;
�����A��ʾ����2����B��ʾ������-2+5=3��A��B�����ľ�����3-(-1)=5��
(2)��m��n���ɵ�M���N֮��ľ���ɱ�ʾΪm��n;
(3)��x��-2������Ҳ�����������ɣ�2���Ĺ�ʽ�ɵ�x��ֵ..
��: ���������
(1)�����A��ʾ��5����B��ʾ������5-4=1,A��B�����ľ�����5-(1)=4;
�����A��ʾ����2����B��ʾ������-2+5=3��A��B�����ľ�����3-(-1)=5��
��2���ɵ�M��Ӧ������m����N��Ӧ������n����m��n���ɵ�M���N֮��ľ���ɱ�ʾΪm��n��
��3���ٵ�x��-2��࣬�ɵ�-2-x=3���ɵ�x=-5��
�ڵ�x��-2��࣬�ɵ�x-��-2��=3��x=1


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
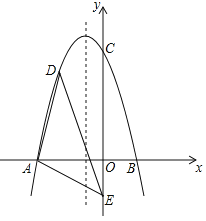
����Ŀ����1����ͼ������ABC�ı�AB��AC������������ABDE��������ACFG�����ж���ABC����AEG���֮��Ĺ�ϵ����˵�����ɡ�

��2����С·������ͨ�ģ���ͼ2��ʾ��С·�ɰ�ɫ����������ʯ�ͺ�ɫ����������ʯ�̳ɣ���֪�м�����������ε����֮����aƽ���ף���Ȧ�����������ε����֮����bƽ���ף�����С·һ��ռ�ض���ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ������һ��
������һ��![]() ������
������![]() .
.
��1������κ����ı���ʽ��
��2������![]() ��������
Ϊ��������![]() �Ḻ�����Ϸ���һ�����㣬��
�Ḻ�����Ϸ���һ�����㣬��![]() ��������ֵ��
��������ֵ��
��3�������߶Գ������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() Ϊ���������Σ������ڣ���ֱ��д������
Ϊ���������Σ������ڣ���ֱ��д������![]() ������꣬����������˵������.
������꣬����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ�٣�AD�ǡ�ABC�����ߣ���ABD���ACD�������������������ϵ��Ϊʲô��
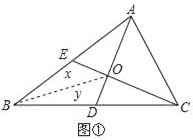
(2)�������ε������ΪS�����磺��ABC�������ΪS��ABC����ͼ�ڣ���֪S��ABC��1����ABC������AD��CE�ཻ�ڵ�O�����ı���BDOE�������
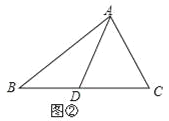
С������(1)�Ľ��ۣ�������������⣬�ⷨ���£�
����BO����S��BEO��x��S��BDO��y����(1)���ۿɵã�S��BCE��S��BAD��![]() S��ABC��
S��ABC��![]() ��S��BCO��2S��BDO��2y��S��BAO��2S��BEO��2x������
��S��BCO��2S��BDO��2y��S��BAO��2S��BEO��2x������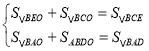 ��
��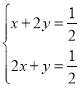 ����x��y��
����x��y��![]() �����ı���BDOE���Ϊ
�����ı���BDOE���Ϊ![]() ��
��
���������ķ���������������⣺
����ͼ�ۣ���֪S��ABC��1��D��E��BC���ϵ����ȷֵ㣬F��G��AB���ϵ����ȷֵ㣬AD��CF���ڵ�O�����ı���BDOF�������
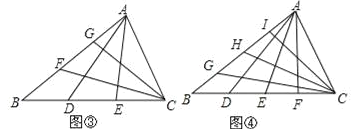
����ͼ�ܣ���֪S��ABC��1��D��E��F��BC���ϵ��ĵȷֵ㣬G��H��I��AB���ϵ��ĵȷֵ㣬AD��CG���ڵ�O�����ı���BDOG�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ʵ����������������������������н���ƻ���������A��B���ֻ��͵������ⷿ����40�ף�Ͷ���ʽ���200��Ԫ���ֲ�����198��Ԫ����������칫��Ԥ�㣺һ��A�������ⷿ�������Ϊ5.2��Ԫ��һ��B�������ⷿ�������Ϊ4.8��Ԫ��
��1�������м��ֿ������跽����
��2�����ֽ��跽��Ͷ���ʽ����٣������ʽ��Ƕ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ж� 600 ����ҵ���п�����������λ��ǰ���ɼ��������������Ƴ� ���²�������ͳ��ͼ��
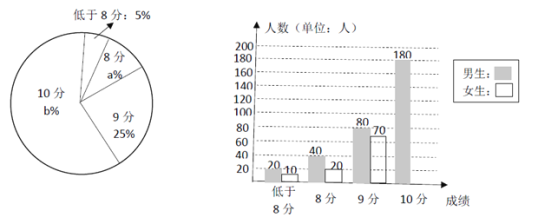
����ͳ��ͼ���ش��������⡣
(1)�뽫����ͳ��ͼ����������
(2)����ͳ��ͼ�У�b= ���� 8 ������Ӧ���ε�Բ�ĽǶ���Ϊ ;
(3)�ڱ��ε����ѧ���У������ȡ 1 �����������ijɼ������� 9 �ֵĸ���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݲ��ϣ��������
��ͼ���������е�![]() ����Ӧ�����ֱ���6��-4��4��-1����
����Ӧ�����ֱ���6��-4��4��-1����![]() �����ľ���Ϊ
�����ľ���Ϊ![]() ��
��![]() �����ľ���Ϊ
�����ľ���Ϊ![]() ��
��![]() �����ľ���Ϊ
�����ľ���Ϊ![]() ���ɴˣ�����������������
���ɴˣ�����������������![]() �ֱ��ʾ������
�ֱ��ʾ������![]() ����
����![]() �����ľ���ɱ�ʾΪ
�����ľ���ɱ�ʾΪ![]() ����֮��
����֮��![]() ��ʾ������
��ʾ������![]() �������ϵĶ�Ӧ��
�������ϵĶ�Ӧ��![]() ֮��ľ��룬��֮Ϊ����ֵ�ļ���������
֮��ľ��룬��֮Ϊ����ֵ�ļ���������
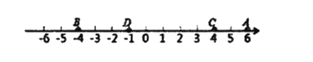
����Ӧ��1��
��1�������ʾ-1�ĵ�![]() �ͱ�ʾ
�ͱ�ʾ![]() �ĵ�
�ĵ�![]() ֮��ľ�����2�����
֮��ľ�����2�����![]() ��Ӧ��
��Ӧ��![]() ��ֵΪ___________��
��ֵΪ___________��
��2������![]() �Ľ�
�Ľ�![]() ____________��
____________��
��3������![]() �Ľ�
�Ľ�![]() ______________ ��
______________ ��
����Ӧ��2��
��ͼ���������ϱ�ʾ![]() �ĵ�Ϊ
�ĵ�Ϊ![]() .
.
��4��![]() �ļ���������������_____________����
�ļ���������������_____________����![]() __________��
__________��![]() ��ֵ��С��____________��
��ֵ��С��____________��
��5��![]() �ļ���������������_______��
�ļ���������������_______��![]() ����Сֵ��__________����ʱ��
����Сֵ��__________����ʱ��![]() ��������Ӧλ��__________�ϣ�
��������Ӧλ��__________�ϣ�
��6����������������������![]() ����Сֵ��___________����ʱ
����Сֵ��___________����ʱ![]() __________��
__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Rt��ABC����C��90�㣬AB��10����cosA��![]() . MΪ�߶�AB���е㣬 ��DM��AB��AC��D. ��Q���߶�AC�ϣ���P���߶�BC�ϣ���PQΪֱ����Բʼ�չ���M�� ��PQ���߶�DM�ڵ�E.
. MΪ�߶�AB���е㣬 ��DM��AB��AC��D. ��Q���߶�AC�ϣ���P���߶�BC�ϣ���PQΪֱ����Բʼ�չ���M�� ��PQ���߶�DM�ڵ�E.
�� ��˵����AMQ�ס�PME��
�� ����PME�ǵ���������ʱ������߶�AQ�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
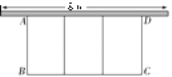
����Ŀ����ͼ����һ�濿ǽ�Ŀյ����ó�Ϊ24 m�����Χ���м���ж�����ʵij����λ��ԣ��軨�ԵĿ�ABΪx m�����ΪS m2.
(1)��S��x�ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
(2)��֪ǽ�������ó���Ϊ8 m��
������Χ�ɻ��Ե���������
������Χ���Ե������С��20 m2����ֱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com