
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
【答案】(1)共有6种方案;(2)当建设A型15套时,投入资金最少,最少资金是198万元.
【解析】(1)设建设A型x套,B型(40﹣x)套,然后根据投入资金不超过200万元,又不低于198万元列出不等式组,求出不等式组的解集,再根据x是正整数解答;
(2)设总投资W元,建设A型x套,B型(40﹣x)套,然后根据总投资等于A、B两个型号的投资之和列式函数关系式,再根据一次函数的增减性解答.
(1)设建设A型x套,则B型(40﹣x)套,根据题意得![]()
![]() ,
,
解不等式①得:x≥15,
解不等式②得:x≤20,
所以不等式组的解集是15≤x≤20.
∵x为正整数,∴x=15、16、17、18、19、20.
答:共有6种方案.
(2)设总投资W万元,建设A型x套,则B型(40﹣x)套,则
W=5.2x+4.8×(40﹣x)=0.4x+192.
∵0.4>0,∴W随x的增大而增大,
∴当x=15时,W最小,此时W最小=0.4×15+192=198万元.
答:当建设A型15套时,投入资金最少,最少资金是198万元.


科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,D是斜边AB上任一点,
,D是斜边AB上任一点,![]() 于E,
于E,![]() 交CD的延长线于点F.
交CD的延长线于点F.![]() 于点H,交AE于点G.
于点H,交AE于点G.

(1)直接写出EF、AE和BF之间的关系;
(2)探究BD与CG之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在下面括号里补充完整证明过程:
已知:如图,△ABC中,∠ACB=90°,AF平分∠CAB,交CD于点E,交CB于点F,且∠CEF=∠CFE.求证:CD⊥AB.
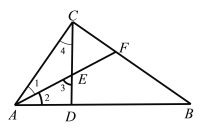
证明:∵AF平分∠CAB (已知)
∴ ∠1=∠2( )
∵∠CEF=∠CFE , 又∠3=∠CEF (对顶角相等)
∴∠CFE=∠3(等量代换)
∵在△ACF中,∠ACF=90°(已知)
∴( )+∠CFE=90°( )
∵∠1=∠2, ∠CFE=∠3(已证) ∴( )+( )=90°(等量代换)
在△AED中, ∠ADE=90°( 三角形内角和定理)
∴ CD⊥AB( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,按要求完成下列各小题.
(1)若A+B的结果中不存在含x的一次项,求a的值;
(2)当a=﹣2时,求A﹣3B的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:数轴上任意两点之间的距离与这两点对应的数的关系.
![]()
(1)如果点A表示数5,将点A先向左移动4个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
如果点A表示数﹣2,将点A向右移动5个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
(2)发现:在数轴上,如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为 (用m、n表示,且m≥n).
(3)应用:利用你发现的结论解决下列问题:数轴上表示x和﹣2的两点P与Q之间的距离是3,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年![]() 月的商品销售总额一共是
月的商品销售总额一共是![]() 万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
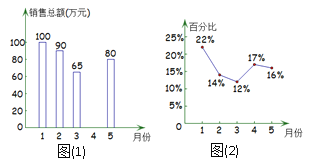
A. 4月份商场的商品销售总额是75万元 B. 1月份商场服装部的销售额是22万元
C. 5月份商场服装部的销售额比4月份减少了 D. 3月份商场服装部的销售额比2月份减少了
查看答案和解析>>
科目:初中数学 来源: 题型:
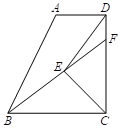
【题目】如图,在四边形ABCD中,∠ADC=∠BCD=90°,BC=CD=2AD,E为∠BCD平分线上的点,连接BE、DE, 延长BE交CD于点F.
⑴ 求证:△BCE≌△DCE;
⑵ 若DE∥AB,求证:FD=FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C是线段AB的中点
(1)如图,若点D在线段CB上,且BD=1.5厘米,AD=6.5厘米,求线段CD的长度;
![]()
(2)若将(1)中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com