
【题目】请在下面括号里补充完整证明过程:
已知:如图,△ABC中,∠ACB=90°,AF平分∠CAB,交CD于点E,交CB于点F,且∠CEF=∠CFE.求证:CD⊥AB.
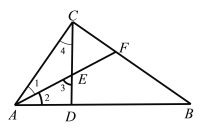
证明:∵AF平分∠CAB (已知)
∴ ∠1=∠2( )
∵∠CEF=∠CFE , 又∠3=∠CEF (对顶角相等)
∴∠CFE=∠3(等量代换)
∵在△ACF中,∠ACF=90°(已知)
∴( )+∠CFE=90°( )
∵∠1=∠2, ∠CFE=∠3(已证) ∴( )+( )=90°(等量代换)
在△AED中, ∠ADE=90°( 三角形内角和定理)
∴ CD⊥AB( ).
【答案】角平分线的定义;∠CAF;直角三角形中两锐角互余;∠2;∠3;垂直的定义
【解析】
首先根据角平分线定义可得∠1=∠2,然后再利用等量代换可得∠CFE=∠3,根据直角三角形中两锐角互余,得到∠CAF+∠CFE=90°,进而可得∠2+∠3=90°,再根据三角形内角和定理得∠ADE=90°,进而得到CD⊥AB.
证明:∵AF平分∠CAB (已知)
∴ ∠1=∠2(角平分线的定义)
∵∠CEF=∠CFE , 又∠3=∠CEF (对顶角相等)
∴∠CFE=∠3(等量代换)
∵在△ACF中,∠ACF=90°(已知)
∴∠CAF+∠CFE=90°(直角三角形中两锐角互余)
∵∠1=∠2, ∠CFE=∠3(已证) ∴(∠2)+(∠3)=90°(等量代换)
在△AED中, ∠ADE=90°(三角形内角和定理)
∴ CD⊥AB(垂直的定义).
故答案为:角平分线的定义;∠CAF;直角三角形中两锐角互余;∠2;∠3;垂直的定义.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知BC∥GE,AF∥DE,∠1=50°.
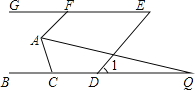
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
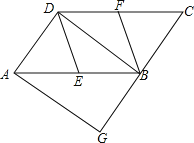
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
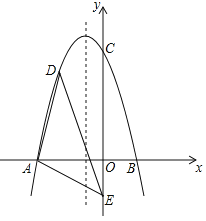
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生对以下四个电视节目:![]() 最强大脑
最强大脑![]() 、
、![]() 中国诗词大会
中国诗词大会![]() 、
、![]() 朗读者
朗读者![]() 、
、![]() 出彩中国人
出彩中国人![]() 的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.
的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.

请你根据图中所提供的信息,完成下列问题:
![]() 本次调查的学生人数为______;
本次调查的学生人数为______;
![]() 在扇形统计图中,A部分所占圆心角的度数为______;
在扇形统计图中,A部分所占圆心角的度数为______;
![]() 请将条形统计图补充完整;
请将条形统计图补充完整;
![]() 若该校共有3000名学生,估计该校最喜爱
若该校共有3000名学生,估计该校最喜爱![]() 中国诗词大会
中国诗词大会![]() 的学生有多少名.
的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系?为什么?
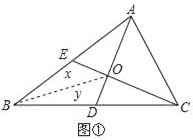
(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC.如图②,已知S△ABC=1.△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.
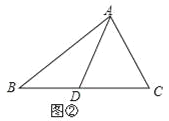
小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,由(1)结论可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有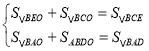 即
即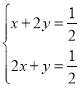 所以x+y=
所以x+y=![]() .即四边形BDOE面积为
.即四边形BDOE面积为![]() .
.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1.D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.
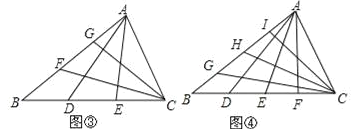
②如图④,已知S△ABC=1.D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据材料,解答问题
如图,数轴上有点![]() ,对应的数分别是6,-4,4,-1,则
,对应的数分别是6,-4,4,-1,则![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;由此,若数轴上任意两点
;由此,若数轴上任意两点![]() 分别表示的数是
分别表示的数是![]() ,则
,则![]() 两点间的距离可表示为
两点间的距离可表示为![]() .反之,
.反之,![]() 表示有理数
表示有理数![]() 在数轴上的对应点
在数轴上的对应点![]() 之间的距离,称之为绝对值的几何意义.
之间的距离,称之为绝对值的几何意义.
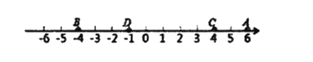
问题应用1:
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为___________;
的值为___________;
(2)方程![]() 的解
的解![]() ____________;
____________;
(3)方程![]() 的解
的解![]() ______________ ;
______________ ;
问题应用2:
如图,若数轴上表示![]() 的点为
的点为![]() .
.
(4)![]() 的几何意义是数轴上_____________,当
的几何意义是数轴上_____________,当![]() __________,
__________,![]() 的值最小是____________;
的值最小是____________;
(5)![]() 的几何意义是数轴上_______,
的几何意义是数轴上_______,![]() 的最小值是__________,此时点
的最小值是__________,此时点![]() 在数轴上应位于__________上;
在数轴上应位于__________上;
(6)根据以上推理方法可求![]() 的最小值是___________,此时
的最小值是___________,此时![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点![]() ,第二次点
,第二次点![]() 跳动至点
跳动至点![]() 第三次点
第三次点![]() 跳动至点
跳动至点![]() ,第四次点
,第四次点![]() 跳动至点
跳动至点![]() ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点![]() 与点
与点![]() 之间的距离是( )
之间的距离是( )

A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com