
【题目】如图,分别以![]() 的斜边
的斜边![]() ,直角边
,直角边![]() 为边向外作等边
为边向外作等边![]() 和
和![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 相交于点
相交于点![]() .若∠BAC=30°,下列结论:①
.若∠BAC=30°,下列结论:①![]() ;②四边形
;②四边形![]() 为平行四边形;③
为平行四边形;③![]() ;④
;④![]() .其中正确结论的序号是______.
.其中正确结论的序号是______.
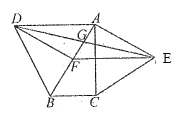
【答案】①②③④
【解析】
首先证明证明Rt△ADF≌Rt△BAC,结合已知得到AE=DF,然后根据内错角相等两直线平行得到DF∥AE,由一组对边平行且相等可得四边形ADFE是平行四边形,故②正确;由∠DAC=∠DAB+∠BAC=90°,可得∠AHE=90°,故①正确;由2AG=AF可知③正确;在Rt△DBF和Rt△EFA中,BD=FE,DF=EA,可证Rt△DBF≌Rt△EFA,故④正确.
∵△ABD和△ACE都是等边三角形,
∴AD=BD=AB,AE=CE=AC,∠ADB=∠BAD=∠DBA=∠CAE=∠AEC=∠ACE=60°.
∵F是AB的中点,
∴∠BDF=∠ADF=30°,∠DFA=∠DFB=90°,BF=AF=![]() AB.
AB.
∵∠BAC=30°,∠ACB=90°,AD=2AF.
∴BC=![]() AB,∠ADF=∠BAC,
AB,∠ADF=∠BAC,
∴AF=BF=BC.
在Rt△ADF和Rt△BAC中
AD=BA ,AF=BC,
∴Rt△ADF≌Rt△BAC(HL),
∴DF=AC,
∴AE=DF.
∵∠BAC=30°,
∴∠BAC+∠CAE=∠BAE=90°,
∴∠DFA=∠EAB,
∴DF∥AE,
∴四边形ADFE是平行四边形,故②正确;
∴AD=EF,AD∥EF,
设AC交EF于点H,
∴∠DAC=∠AHE.
∵∠DAC=∠DAB+∠BAC=90°,
∴∠AHE=90°,
∴EF⊥AC.①正确;
∵四边形ADFE是平行四边形,
∴2GF=2GA=AF.
∴AD=4AG.故③正确.
在Rt△DBF和Rt△EFA中
BD=FE,DF=EA,
∴Rt△DBF≌Rt△EFA(HL).故④正确,
故答案为:①②③④.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场购进了一批![]() 、
、![]() 两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
类型 | 进购数量(个) | 进价(元/个) | 售价(元/个) |
| 20 | 1800 | 2300 |
| 40 | 1500 | ? |
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元,则![]() 型智能扫地机器人的销售单价至少是多少元?
型智能扫地机器人的销售单价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
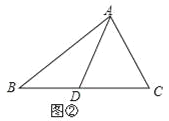
【题目】(1)如图①,AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系?为什么?
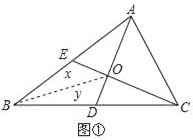
(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC.如图②,已知S△ABC=1.△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.
小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,由(1)结论可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有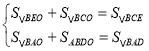 即
即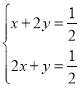 所以x+y=
所以x+y=![]() .即四边形BDOE面积为
.即四边形BDOE面积为![]() .
.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1.D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.
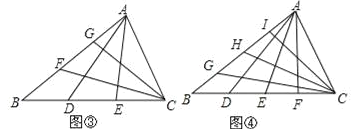
②如图④,已知S△ABC=1.D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中对 600 名毕业生中考体育测试坐位体前屈成绩进行整理,绘制成 如下不完整的统计图:
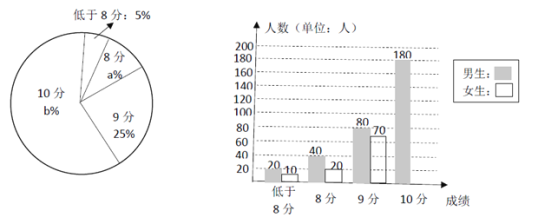
根据统计图,回答下列问题。
(1)请将条形统计图补充完整;
(2)扇形统计图中,b= ,得 8 分所对应扇形的圆心角度数为 ;
(3)在本次调查的学生中,随机抽取 1 名男生,他的成绩不低于 9 分的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据材料,解答问题
如图,数轴上有点![]() ,对应的数分别是6,-4,4,-1,则
,对应的数分别是6,-4,4,-1,则![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;由此,若数轴上任意两点
;由此,若数轴上任意两点![]() 分别表示的数是
分别表示的数是![]() ,则
,则![]() 两点间的距离可表示为
两点间的距离可表示为![]() .反之,
.反之,![]() 表示有理数
表示有理数![]() 在数轴上的对应点
在数轴上的对应点![]() 之间的距离,称之为绝对值的几何意义.
之间的距离,称之为绝对值的几何意义.
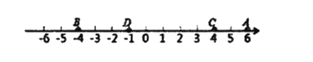
问题应用1:
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为___________;
的值为___________;
(2)方程![]() 的解
的解![]() ____________;
____________;
(3)方程![]() 的解
的解![]() ______________ ;
______________ ;
问题应用2:
如图,若数轴上表示![]() 的点为
的点为![]() .
.
(4)![]() 的几何意义是数轴上_____________,当
的几何意义是数轴上_____________,当![]() __________,
__________,![]() 的值最小是____________;
的值最小是____________;
(5)![]() 的几何意义是数轴上_______,
的几何意义是数轴上_______,![]() 的最小值是__________,此时点
的最小值是__________,此时点![]() 在数轴上应位于__________上;
在数轴上应位于__________上;
(6)根据以上推理方法可求![]() 的最小值是___________,此时
的最小值是___________,此时![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
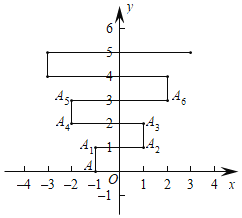
【题目】如图,在平面直角坐标系上有个点A(﹣1,0),点A第1次向上跳动1个单位至点A1(﹣1,1),紧接着第2次向右跳动2个单位至点A2(1,1),第3次向上跳动1个单位至点A3,第4次向左跳动3个单位至点A4,第5次又向上跳动1个单位至点A5,第6次向右跳动4个单位至点A6,……,依此规律跳动下去,点A第2019次跳动至点A2019的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC,∠C=90°,AB=10,且cosA=![]() . M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
. M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
⑴ 试说明△AMQ∽△PME;
⑵ 当△PME是等腰三角形时,求出线段AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求下列函数的图象的对称轴、顶点坐标及与x轴的交点坐标.
(1)y=4x2+24x+35;
(2)y=-3x2+6x+2;
(3)y=x2-x+3;
(4)y=2x2+12x+18.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com