
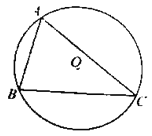
【题目】如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
【答案】(1)画图见解析;(2)CE=![]()
【解析】(1)以点A为圆心,以任意长为半径画弧,分别与AB、AC有交点,再分别以这两个交点为圆心,以大于这两点距离的一半为半径画弧,两弧交于一点,过点A与这点作射线,与圆交于点E ,据此作图即可;
(2)连接OE交BC于点F,连接OC、CE,由AE平分∠BAC,可推导得出OE⊥BC,然后在Rt△OFC中,由勾股定理可求得FC的长,在Rt△EFC中,由勾股定理即可求得CE的长.
(1)如图所示,射线AE就是所求作的角平分线;
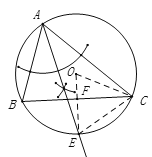
(2)连接OE交BC于点F,连接OC、CE,
∵AE平分∠BAC,
∴![]() ,
,
∴OE⊥BC,EF=3,∴OF=5-3=2,
在Rt△OFC中,由勾股定理可得FC=![]() =
=![]() ,
,
在Rt△EFC中,由勾股定理可得CE=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知Rt△ABC,∠C=90°,AB=10,且cosA=![]() . M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
. M为线段AB的中点, 作DM⊥AB交AC于D. 点Q在线段AC上,点P在线段BC上,以PQ为直径的圆始终过点M, 且PQ交线段DM于点E.
⑴ 试说明△AMQ∽△PME;
⑵ 当△PME是等腰三角形时,求出线段AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
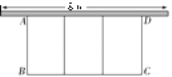
【题目】如图,在一面靠墙的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
(1)求S与x的函数关系式及自变量的取值范围;
(2)已知墙的最大可用长度为8 m,
①求所围成花圃的最大面积;
②若所围花圃的面积不小于20 m2,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段![]() (点A,B的对应点分别为
(点A,B的对应点分别为![]() ).画出线段
).画出线段![]() ;
;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() .画出线段
.画出线段![]() ;
;
(3)以![]() 为顶点的四边形
为顶点的四边形![]() 的面积是 个平方单位.
的面积是 个平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
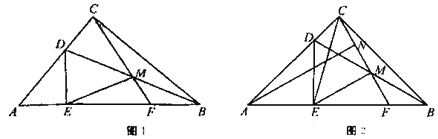
【题目】如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F.
(1)求证:CM=EM;
(2)若∠BAC=50°,求∠EMF的大小;
(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.
查看答案和解析>>
科目:初中数学 来源: 题型:
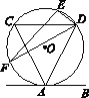
【题目】如图,直线AB与⊙O相切于点A,弦CD∥AB,E、F为圆上的两点,且∠CDE=∠ADF.若⊙O的半径为![]() ,CD=4,则弦EF的长为( )
,CD=4,则弦EF的长为( )
A. 4 B. 2![]()
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠ABC和∠ACB的角平分线交于O,且∠ABC的角平分线与∠ACB的外角平分线交于P,∠OPC和∠OCP角平分线交于H,∠H=117.5°,则∠A=________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个长方体纸盒 平面展开图,已知纸盒中相对两个面上的数互为相反数
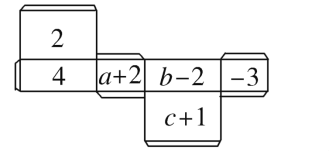
(1)填空:![]() __________,
__________,![]() ___________,
___________,![]() ___________.
___________.
(2)先化简,再求值:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com