
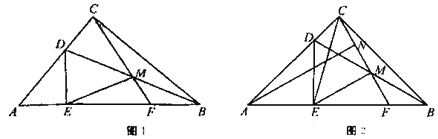
【题目】如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F.
(1)求证:CM=EM;
(2)若∠BAC=50°,求∠EMF的大小;
(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.
【答案】(1)证明见解析;(2)∠EMF=100°;(3)证明见解析.
【解析】(1)在Rt△DCB和Rt△DEB中,利用直角三角形斜边中线等于斜边一半进行证明即可得;
(2)根据直角三角形两锐角互余可得∠ABC=40°,根据CM=MB,可得∠MCB=∠CBM,从而可得∠CMD=2∠CBM,继而可得∠CME=2∠CBA=80°,根据邻补角的定义即可求得∠EMF的度数;
(3)由△DAE≌△CEM,CM=EM,∠DEA=90°,结合CM=DM以及已知条件可得△DEM是等边三角形,从而可得∠EDM=60°,∠MBE=30°,继而可得∠ACM=75°,连接AM,结合AE=EM=MB,可推导得出AC=AM,根据N为CM中点,可得AN⊥CM,再根据CM⊥EM,即可得出AN∥EM.
(1)∵M为BD中点,
Rt△DCB中,MC=![]() BD,
BD,
Rt△DEB中,EM=![]() BD,
BD,
∴MC=ME;
(2)∵∠BAC=50°,∠ACB=90°,
∴∠ABC=90°-50°=40°,
∵CM=MB,
∴∠MCB=∠CBM,
∴∠CMD=∠MCB+∠CBM=2∠CBM,
同理,∠DME=2∠EBM,
∴∠CME=2∠CBA=80°,
∴∠EMF=180°-80°=100°;
(3)∵△DAE≌△CEM,CM=EM,
∴AE=EM,DE=CM,∠CME=∠DEA=90°,∠ECM=∠ADE,
∵CM=EM,∴AE=ED,∴∠DAE=∠ADE=45°,
∴∠ABC=45°,∠ECM=45°,
又∵CM=ME=![]() BD=DM,
BD=DM,
∴DE=EM=DM,
∴△DEM是等边三角形,
∴∠EDM=60°,
∴∠MBE=30°,
∵CM=BM,∴∠BCM=∠CBM,
∵∠MCB+∠ACE=45°,
∠CBM+∠MBE=45°,
∴∠ACE=∠MBE=30°,
∴∠ACM=∠ACE+∠ECM=75°,
连接AM,∵AE=EM=MB,
∴∠MEB=∠EBM=30°,
∠AME=![]() ∠MEB=15°,
∠MEB=15°,
∵∠CME=90°,
∴∠CMA=90°-15°=75°=∠ACM,
∴AC=AM,
∵N为CM中点,
∴AN⊥CM,
∵CM⊥EM,
∴AN∥CM.


科目:初中数学 来源: 题型:
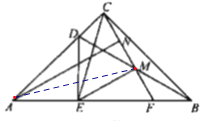
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.

(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.



(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
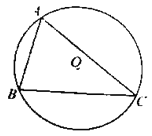
【题目】如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
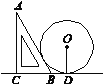
【题目】如图,一块直角三角板ABC(∠A=30°)的斜边AB与一个以r为半径的圆轮子相靠,若BD=1,则r等于( )
A. 2 B. ![]() C. 1.5 D.
C. 1.5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,O,D分别为AB,BC上的点,经过A,D两点的⊙O分别交AB,AC于点E,F,且D为弧EF的中点.
(1)求证:BC与⊙O相切;
(2)当⊙O的半径r=2,∠CAD=30°时,求劣弧AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店,甲种笔记本标价每本8元,乙种笔记本标价每本5元.今天,甲、乙两种笔记本合计卖了100本,共卖了695元!
(1)两种笔记本各销售了多少?
(2)所得销售款可能是660元吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com