
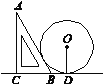
【题目】如图,一块直角三角板ABC(∠A=30°)的斜边AB与一个以r为半径的圆轮子相靠,若BD=1,则r等于( )
A. 2 B. ![]() C. 1.5 D.
C. 1.5 D. ![]()
【答案】B
【解析】记⊙O与直角三角尺的斜边切于点E,连结OB,OE,由已知可求出∠ABC的度数,进而可求出∠ABD的度数,由已知不难证得△OEB≌△ODB,再利用全等三角形的性质,结合直角三角形的两个锐角互余,求出∠OBD、∠BOD的度数,在Rt△ODB中,由特殊角所对的直角边与斜边的关系,利用直角三角形的勾股定理即可求解.
记⊙O与△ABC切于点E,连结OE、OB.
∵ 在Rt△ACB中,∠C=90°,∠A=30°
∴ ∠ABC=60° (直角三角形的两个锐角互余)
∵ ∠ABC+∠ABD=180°,∠ABC=60°,
∴ ∠ABD=120°,
∵ AB、BD与⊙O分别相切于点E、D.
∴ OE⊥AB OD⊥BD (过切点及圆心的线段垂直于该切线)
∴ △OEB和△ODB是直角三角形 (两边相互垂直的三角形是直角三角形)
∵ BE、BD是过点B的⊙O的两条切线,
∴ BE=BD (切线长定理)
∵ BE=BD OB=OB
∴ Rt△OEB≌Rt△ODB (HL)
∴ ∠OBE=∠OBD (全等三角形的对应角相等)
∵ ∠ABD=120° ,∠OBE=∠OBD
∴ ∠OBE=∠OBD=60°
∵ ∠ODB=90° ,∠OBD=60°
∴ ∠BOD=30° (直角三角形的两个锐角互余)
∵ ∠ODB=90° ,BOD=30°
∴ BD=![]() ×OB (在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)
×OB (在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)
∵ BD=BD=![]() ×OB
×OB
∴ OB=2,
∵ ∠ODB=90° ,BD=1,OB=2,
∴ OD=![]() (直角三角形勾股定理求值)
(直角三角形勾股定理求值)
即r=![]()
故选:B.


科目:初中数学 来源: 题型:
【题目】老师在讲“实数”时画了一个图(如图),即“以数轴的单位长度为边作一个正方形,然后以原点为圆心,正方形的对角线长为半径画弧交数轴于点A.

(1)A点表示的数是多少?在数轴上,A点与表示一1.42的点有什么位置关系;
(2)你认为老师作这样的图是为了说明什么?
(3)请类比上面的作法在数轴上画出表示-![]() 的点B.(请保留作图痕迹)
的点B.(请保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
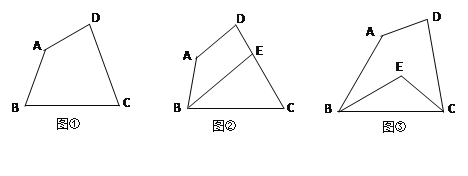
【题目】四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)

查看答案和解析>>
科目:初中数学 来源: 题型:
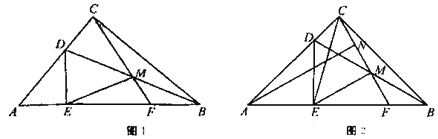
【题目】如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F.
(1)求证:CM=EM;
(2)若∠BAC=50°,求∠EMF的大小;
(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为a,点B对应的数为b,点A在负半轴,且|a|=6,b是最小的正偶数.
(1)求线段AB的长;
(2)若点C在数轴上对应的数为x,且x是方程2x+1=3x-9的解,在数轴上是否存在点P,使得PA+PB=![]() BC+AB,若存在,求出点P对应的数,若不存在,说明理由.
BC+AB,若存在,求出点P对应的数,若不存在,说明理由.
(3)如图,若Q是B点右侧一点,QA的中点为M,N为QB的四等分点且靠近于Q点,当Q在B的右侧运动时,说明:QM﹣![]() BN的值不变,并求出其值.
BN的值不变,并求出其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今有三部自动换币机,其中甲机总是将一枚硬币换成2枚其他硬币;乙机总是将一枚硬币换成4枚其他硬币;丙机总是将一枚硬币换面10枚其他硬币.某人共进行了12次换币,便将一枚硬币换成了81枚.试问他在丙机上换了_____次?
查看答案和解析>>
科目:初中数学 来源: 题型:
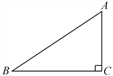
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)分别以直线AC,BC为轴,把△ABC旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;
(2)以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com