
����Ŀ�������ϵ�A��Ӧ����Ϊa����B��Ӧ����Ϊb����A�ڸ����ᣬ��|a|=6��b����С����ż����
��1�����߶�AB�ij���
��2������C�������϶�Ӧ����Ϊx����x�Ƿ���2x+1=3x��9�Ľ⣬���������Ƿ���ڵ�P��ʹ��PA��PB��![]() BC��AB�������ڣ������P��Ӧ�������������ڣ�˵�����ɣ�
BC��AB�������ڣ������P��Ӧ�������������ڣ�˵�����ɣ�
��3����ͼ����Q��B���Ҳ�һ�㣬QA���е�ΪM��NΪQB���ĵȷֵ��ҿ�����Q�㣬��Q��B���Ҳ��˶�ʱ��˵����QM��![]() BN��ֵ���䣬�������ֵ��
BN��ֵ���䣬�������ֵ��
![]()
���𰸡���1��8����2�����ڣ���P��Ӧ����Ϊ-8��4����3��4
��������
��1���ȸ����������a��b��ֵ������AB�ij���
��2���Ƚⷽ�����x��ֵ���ó���C�������϶�Ӧ�������Ӷ��ó�PA+PB=12�����P�Ķ�Ӧ��Ϊm���ٷ�3��������۷������ֱ���ʽ���㼴�ɣ�
��3�����Q�Ķ�Ӧ��Ϊt���ú�t��ʽ�ӱ�ʾ��QM��BN����֤�����ۣ�
�⣺��1��������ã�a=-6��b=2��
��AB=2-(-6)=8��
��2����2x+1=3x��9
��ã�x=10
���C��Ӧ����Ϊ10��
��BC=10-2=8��AB=2-(-6)=8��
��![]() BC��AB=12=PA��PB
BC��AB=12=PA��PB
���P�Ķ�Ӧ��Ϊm��
�ٵ�P��A���ʱ��-6-m+2-m=12����ã�m=-8��
�ڵ�P��A�Ҳ�ʱ��6+m+m-2=12����ã�m=4��
�۵�P��AB֮��ʱ��PA+PB=8��ȥ��
���P�Ķ�Ӧ��Ϊ-8��4��
��3�����Q�Ķ�Ӧ��Ϊt��
��QA=t-(-6)=t+6��QB=t-2
��MΪQA���е�
��![]()
��NΪQB���ĵȷֵ�
��![]()
��![]()
��QM��![]() BN��ֵ���䣬��ֵΪ4��
BN��ֵ���䣬��ֵΪ4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ι�˾�ھ�����������50���۹���ο�����ʹ�ã��ٶ�ÿ���۹һ�������ֻ�ܳ���һ�Σ���ÿ�����������x��Ԫ����5�ı���������ÿ���Ӫ�˹������£���x������100Ԫʱ���۹��ȫ���������x����100Ԫʱ��ÿ�����������ÿ����5Ԫ�����ȥ�Ĺ۹�ͻ����1������֪���й۹ÿ��Ĺ�������1100Ԫ��
��1���Żݻ�ڼ䣬Ϊʹ�۹ȫ�������ÿ��ľ�����Ϊ������ÿ���������������ӦΪ����Ԫ����ע��������=������������ѣ�
��2����ÿ�����������Ϊ����Ԫʱ��ÿ��ľ�������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��AB��DC����PΪƽ����һ�㣬����AP��CP��



��1����ͼ1����P��ֱ��AB��CD֮�䣬����BAP=60�㣬��DCP=20��ʱ�����APC��
��2����ͼ2����P��ֱ��AB��CD֮�䣬��BAP���DCP�Ľ�ƽ�����ཻ�ڵ�K��д����AKC���APC֮���������ϵ����˵�����ɣ�
��3����ͼ3����P����CD�⣬��BAP���DCP�Ľ�ƽ�����ཻ�ڵ�K����AKC���APC�к�������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ֱ�����ǰ�ABC(��A��30��)��б��AB��һ����rΪ�뾶��Բ���������BD��1����r����(����)
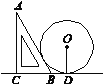
A. 2 B. ![]() C. 1.5 D.
C. 1.5 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC������C��90�㣬O��D�ֱ�ΪAB��BC�ϵĵ�������A��D����ġ�O�ֱ�AB��AC�ڵ�E��F����DΪ��EF���е㣮
(1)��֤��BC���O���У�
(2)����O�İ뾶r��2����CAD��30��ʱ�����ӻ�AD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
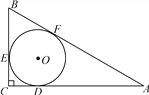
����Ŀ����ͼ����OΪ��ABC������Բ���е�ֱ�ΪD��E��F����C��90�㣬BC��3��AC��4.
(1)���ABC�������
(2)���O�İ뾶��
(3)��AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľߵ꣬���ֱʼDZ����ÿ��8Ԫ�����ֱʼDZ����ÿ��5Ԫ�����죬�ס������ֱʼDZ��ϼ�����100����������695Ԫ!
��1�����ֱʼDZ��������˶��٣�
��2���������ۿ������660Ԫ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
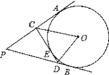
����Ŀ����ͼ��PA��PB�ǡ�O�����ߣ�CD�С�O�ڵ�E����PCD���ܳ�Ϊ12����APB=60����
��1��PA�ij���
��2����COD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
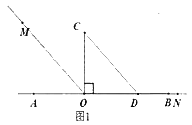
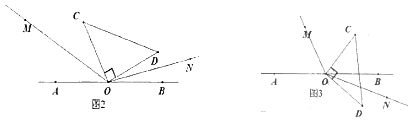
����Ŀ�������龳:��ֱ��AB��һ��OΪ�˵�������OM��ON����һ��ֱ�������ε�ֱ�Ƕ������O��(��COD=90��).
(1)��ͼ1��ֱ�����ǰ�COD�ı�OD��������OB�ϣ�OMƽ�֡�AOC��ON��OB�غϣ����MON=_����
(2)ֱ�����ǰ�COD�Ƶ�O��ת����ͼ2��λ�ã�OMƽ�֡�AOC��ONƽ�֡�BOD�����MON�Ķ�����
(3)ֱ�����ǰ�COD�Ƶ�O��ת����ͼ3��λ�ã�OMƽ�֡� AOC ��ONƽ�֡�BOD�������MON�Ķ�������˵�����ɡ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com