
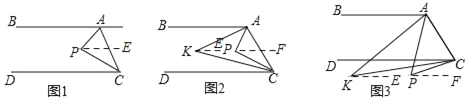
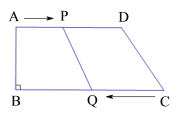
ЁОЬтФПЁПвбжЊЃЌжБЯпABЁЮDCЃЌЕуPЮЊЦНУцЩЯвЛЕуЃЌСЌНгAPгыCPЃЎ



ЃЈ1ЃЉШчЭМ1ЃЌЕуPдкжБЯпABЁЂCDжЎМфЃЌЕБЁЯBAP=60ЁуЃЌЁЯDCP=20ЁуЪБЃЌЧѓЁЯAPCЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕуPдкжБЯпABЁЂCDжЎМфЃЌЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌаДГіЁЯAKCгыЁЯAPCжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌЕуPТфдкCDЭтЃЌЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌЁЯAKCгыЁЯAPCгаКЮЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ80ЁуЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉМћНтЮі
ЁОНтЮіЁПећЬхЗжЮіЃК
ЗжБ№Й§ЕуPЃЌKзїABЕФЦНааЯпЃЌРћгУЦНааЯпЕФаджЪКЭНЧЦНЗжЯпЕФЖЈвхМДПЩЧѓНт.
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЙ§PзїPEЁЮABЃЌ
ЁпABЁЮCDЃЌ
ЁрPEЁЮABЁЮCDЃЌ
ЁрЁЯAPE=ЁЯBAPЃЌЁЯCPE=ЁЯDCPЃЌ
ЁрЁЯAPC=ЁЯAPE+ЁЯCPE=ЁЯBAP+ЁЯDCP=60Ёу+20Ёу=80ЁуЃЛ
ЃЈ2ЃЉЁЯAKC=![]() ЁЯAPCЃЎ
ЁЯAPCЃЎ
РэгЩЃКШчЭМ2ЃЌЙ§KзїKEЁЮABЃЌ
ЁпABЁЮCDЃЌ
ЁрKEЁЮABЁЮCDЃЌ
ЁрЁЯAKE=ЁЯBAKЃЌЁЯCKE=ЁЯDCKЃЌ
ЁрЁЯAKC=ЁЯAKE+ЁЯCKE=ЁЯBAK+ЁЯDCKЃЌ
Й§PзїPFЁЮABЃЌ
ЭЌРэПЩЕУЃЌЁЯAPC=ЁЯBAP+ЁЯDCPЃЌ
ЁпЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌ
ЁрЁЯBAK+ЁЯDCK=![]() ЁЯBAP+
ЁЯBAP+![]() ЁЯDCP=
ЁЯDCP=![]() ЃЈЁЯBAP+ЁЯDCPЃЉ=
ЃЈЁЯBAP+ЁЯDCPЃЉ=![]() ЁЯAPCЃЌ
ЁЯAPCЃЌ
ЁрЁЯAKC=![]() ЁЯAPCЃЛ
ЁЯAPCЃЛ
ЃЈ3ЃЉЁЯAKC=![]() ЁЯAPCЃЎ
ЁЯAPCЃЎ
РэгЩЃКШчЭМ3ЃЌЙ§KзїKEЁЮABЃЌ
ЁпABЁЮCDЃЌ
ЁрKEЁЮABЁЮCDЃЌ
ЁрЁЯBAK=ЁЯAKEЃЌЁЯDCK=ЁЯCKEЃЌ
ЁрЁЯAKC=ЁЯAKEЉЁЯCKE=ЁЯBAKЉЁЯDCKЃЌ
Й§PзїPFЁЮABЃЌ
ЭЌРэПЩЕУЃЌЁЯAPC=ЁЯBAPЉЁЯDCPЃЌ
ЁпЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌ
ЁрЁЯBAKЉЁЯDCK=![]() ЁЯBAPЉ
ЁЯBAPЉ![]() ЁЯDCP=
ЁЯDCP=![]() ЃЈЁЯBAPЉЁЯDCPЃЉ=
ЃЈЁЯBAPЉЁЯDCPЃЉ=![]() ЁЯAPCЃЌ
ЁЯAPCЃЌ
ЁрЁЯAKC=![]() ЁЯAPCЃЎ
ЁЯAPCЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
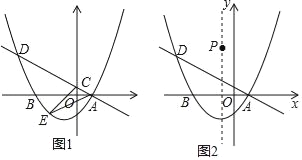
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2+bxЉ![]() гыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉСНЕуЃЌЯжгаОЙ§ЕуAЕФжБЯпlЃКy=kx+b1гыyжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэИіНЛЕуЮЊDЃЎ
гыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉСНЕуЃЌЯжгаОЙ§ЕуAЕФжБЯпlЃКy=kx+b1гыyжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэИіНЛЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєЕуDдкЕкЖўЯѓЯоЧвТњзуCD=5ACЃЌЧѓДЫЪБжБЯп1ЕФНтЮіЪНЃЛдкДЫЬѕМўЯТЃЌЕуEЮЊжБЯп1ЯТЗНХзЮяЯпЩЯЕФвЛЕуЃЌЧѓЁїACEУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕуEЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЃЌЩшPдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвдкЕкЖўЯѓЯоЃЌЕНxжсЕФОрРыЮЊ4ЃЌЕуQдкХзЮяЯпЩЯЃЌШєвдЕуAЃЌDЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮФмЗёГЩЮЊЦНааЫФБпаЮЃПШєФмЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
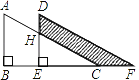
ЁОЬтФПЁПШчЭМЃЌСНИіДѓаЁвЛбљЕФжБНЧШ§НЧаЮжиЕўдквЛЦ№ЃЌНЋЦфжавЛИіШ§НЧаЮбизХЕуBЕНЕуCЕФЗНЯђЦНвЦЕНЁїDEFЕФЮЛжУЃЌABЃН10ЃЌDHЃН4ЃЌЦНвЦОрРыЮЊ6ЃЌдђвѕгАВПЗжУцЛ§ЪЧ_____
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЕФжмГЄЪЧ20ЃЌOBКЭOCЗжБ№ЦНЗжЁЯABCКЭЁЯACBЃЌODЁЭBCгкЕуDЃЌЧвOD=3ЃЌдђЁїABCЕФУцЛ§ЪЧЃЈЁЁЁЁЃЉ

A. 20 B. 25 C. 30 D. 35
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЖгОйааСЫвЛФъвЛЖШЕФШќСњжлБШШќЃЌСНЖгдкБШШќЪБЕФТЗГЬsЃЈУзЃЉгыЪБМфtЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЙиЯЕЭМЯѓШчЭМЫљЪОЃЌЧыФуИљОнЭМЯѓХаЖЯЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. МзЖгТЪЯШЕНДяжеЕу B. МзЖгБШввЖгЖрзпСЫ200УзТЗГЬ
C. ввЖгБШМзЖгЩйгУ0.2Зжжг D. БШШќжаСНЖгДгГіЗЂЕН2.2ЗжжгЪБМфЖЮЃЌввЖгЕФЫйЖШБШМзЖгЕФЫйЖШПь
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂй,дке§ЗНаЮABCDжаЃЌЕуPвд1cm/sЕФЫйЖШДгЕуAГіЗЂАДМ§ЭЗЗНЯђдЫЖЏЃЌЕНДяЕуDЭЃжЙ. ЁїPADЕФУцЛ§y(cm)гыдЫЖЏЪБМфx(s)жЎМфЕФКЏЪ§ЭМЯёШчЭМЂкЫљЪО.(ЙцЖЈ:ЕуPдкЕуAЃЌDЪБЃЌy=0ЃЉ
ЗЂЯж:(1)AB= _______cmЃЌЕБx=17ЪБЃЌy=_________cm2ЃЛ
(2)ЕБЕуPдкЯпЖЮ_________ЩЯдЫЖЏЪБЃЌyЕФжЕБЃГжВЛБф.
ЭиеЙ:ЧѓЕБ0<x<6МА12<x<18ЪБЃЌyгыxжЎМфЕФКЏЪ§ЙиЯЕЪН.
ЬНОП:ЕБxЮЊЖрЩйЪБЃЌyЕФжЕЮЊ15ЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
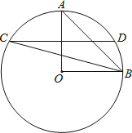
ЁОЬтФПЁПШчЭМЃЌOAЃЎOBЪЧЁбOЕФАыОЖЧвOAЁЭOBЃЌзїOAЕФДЙжБЦНЗжЯпНЛЁбOгкЕуCЃЎDЃЌСЌНгCBЃЎABЃЎ
ЧѓжЄЃКЁЯABC=2ЁЯCBOЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
ЃЈ1ЃЉaКЭ0ЖМЪЧЕЅЯюЪН
ЃЈ2ЃЉЖрЯюЪН![]() ЕФДЮЪ§ЪЧ3
ЕФДЮЪ§ЪЧ3
ЃЈ3ЃЉЕЅЯюЪН![]() ЕФЯЕЪ§ЪЧ
ЕФЯЕЪ§ЪЧ![]()
ЃЈ4ЃЉx2+2xyЃy2ПЩЖСзїx2ЁЂ2xyЁЂЃy2ЕФКЭ
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯB=90ЁуЃЌAB=8![]() ЃЌAD=24
ЃЌAD=24![]() ЃЌBC=26
ЃЌBC=26![]() ЃЌЕуPДгЕуAГіЗЂЃЌвд1
ЃЌЕуPДгЕуAГіЗЂЃЌвд1![]() ЕФЫйЖШЯђЕуDдЫЖЏЃЛЕуQДгЕуCЭЌЪБГіЗЂЃЌвд3
ЕФЫйЖШЯђЕуDдЫЖЏЃЛЕуQДгЕуCЭЌЪБГіЗЂЃЌвд3![]() ЕФЫйЖШЯђЕуBдЫЖЏЃЌЙцЖЈЦфжавЛИіЖЏЕуЕНДяЖЫЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏ.ЩшдЫЖЏЪБМфЮЊ
ЕФЫйЖШЯђЕуBдЫЖЏЃЌЙцЖЈЦфжавЛИіЖЏЕуЕНДяЖЫЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏ.ЩшдЫЖЏЪБМфЮЊ![]()
![]() .
.
ЃЈ1ЃЉ![]() ЮЊКЮжЕЪБЃЌЫФБпаЮPQCDЮЊЦНааЫФБпаЮ?
ЮЊКЮжЕЪБЃЌЫФБпаЮPQCDЮЊЦНааЫФБпаЮ?
ЃЈ2ЃЉ![]() ЮЊКЮжЕЪБЃЌЫФБпаЮPQCDЮЊЕШбќЬнаЮЃПЃЈЕШбќЬнаЮЕФСНбќЯрЕШЃЌСНЕзНЧЯрЕШЃЉ.
ЮЊКЮжЕЪБЃЌЫФБпаЮPQCDЮЊЕШбќЬнаЮЃПЃЈЕШбќЬнаЮЕФСНбќЯрЕШЃЌСНЕзНЧЯрЕШЃЉ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com