
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8![]() ,AD=24
,AD=24![]() ,BC=26
,BC=26![]() ,点P从点A出发,以1
,点P从点A出发,以1![]() 的速度向点D运动;点Q从点C同时出发,以3
的速度向点D运动;点Q从点C同时出发,以3![]() 的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为
的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为![]()
![]() .
.
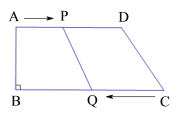
(1)![]() 为何值时,四边形PQCD为平行四边形?
为何值时,四边形PQCD为平行四边形?
(2)![]() 为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等).
为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等).
【答案】(1)6s;(2)7s
【解析】
(1)根据题意可得PA=t,CQ=3t,则PD=AD-PA=24-t,当PD=CQ时,四边形PQCD为平行四边形,可得方程24-t=3t,解此方程即可求得答案;
(2)过点D作DE⊥BC,则CE=BC-AD=2cm当CQ-PD=4时,四边形PQCD是等腰梯形.即3t-(24-t)=4,求出t的值即可.
(1)运动时间为ts.
AP=t,PD=24-t,CQ=3t,
∵经过ts四边形PQCD平行四边形
∴PD=CQ,即24-t=3t,解得t=6.
当t=6s时,四边形PQCD是平行四边形;
(2)如图,过点D作DE⊥BC,则CE=BC-AD=2cm

∵当CQ-PD=4时,四边形PQCD是等腰梯形.即3t-(24-t)=4,
∴t=7.
∴经过7s四边形PQCD是等腰梯形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.



(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
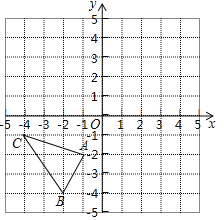
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移3个单位后得到△A1B1C1,请画出△A1B1C1并写出点B1的坐标;
(2)已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2,并直接写出直线l的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
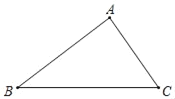
【题目】如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6.
(1)尺规作图:在BC上求作一点P,使点P到点A、B的距离相等;(保留作图痕迹,不写作法和证明)
(2)在(1)的条件下,连接AP,求△APC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
查看答案和解析>>
科目:初中数学 来源: 题型:
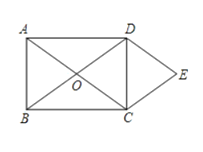
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD
(1)判断四边形OCED是什么特殊四边形?并证明你的结论
(2)当AB、AD满足什么条件时,四边形OCED是正方形?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
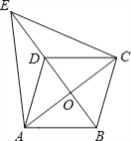
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com