
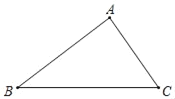
【题目】如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6.
(1)尺规作图:在BC上求作一点P,使点P到点A、B的距离相等;(保留作图痕迹,不写作法和证明)
(2)在(1)的条件下,连接AP,求△APC的周长.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点P以1cm/s的速度从点A出发按箭头方向运动,到达点D停止. △PAD的面积y(cm)与运动时间x(s)之间的函数图像如图②所示.(规定:点P在点A,D时,y=0)
发现:(1)AB= _______cm,当x=17时,y=_________cm2;
(2)当点P在线段_________上运动时,y的值保持不变.
拓展:求当0<x<6及12<x<18时,y与x之间的函数关系式.
探究:当x为多少时,y的值为15?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BE平分∠ABC,CD平分∠ACB,CD交BE 于点F,那么图中的等腰三角形共有( )个.
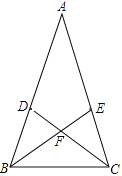
A. 6B. 7C. 8D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8![]() ,AD=24
,AD=24![]() ,BC=26
,BC=26![]() ,点P从点A出发,以1
,点P从点A出发,以1![]() 的速度向点D运动;点Q从点C同时出发,以3
的速度向点D运动;点Q从点C同时出发,以3![]() 的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为
的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为![]()
![]() .
.
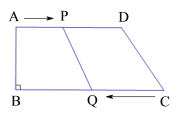
(1)![]() 为何值时,四边形PQCD为平行四边形?
为何值时,四边形PQCD为平行四边形?
(2)![]() 为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等).
为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列四个结论:①AP=EF,②△APD一定是等腰三角形,③∠PFE=∠BAP,④PD=![]() EC.其中正确结论的序号是( )
EC.其中正确结论的序号是( )

A.①②④B.②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
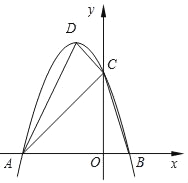
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为底的等腰三角形,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com