
【题目】某文具店,甲种笔记本标价每本8元,乙种笔记本标价每本5元.今天,甲、乙两种笔记本合计卖了100本,共卖了695元!
(1)两种笔记本各销售了多少?
(2)所得销售款可能是660元吗?为什么?
【答案】(1)甲种笔记本销售了65本,则乙种笔记本销售了35本;(2)不可能是660元,理由见解析
【解析】
(1)设甲种笔记本销售了x本,则乙种笔记本销售了(100-x)本,根据总价=单价×数量,即可得出关于x的一元一次方程,求解即可;
(2)设甲种笔记本销售了![]() 本,则乙种笔记本销售了
本,则乙种笔记本销售了![]() 本.根据销售款为660列方程,求出y,若y是正整数则为可能,否则不可能.
本.根据销售款为660列方程,求出y,若y是正整数则为可能,否则不可能.
解:(1)设甲笔记本销售了![]() 本,则乙笔记本销售了
本,则乙笔记本销售了![]() 本,
本,
由题意得![]() ,
,
解得![]() ,
,![]() .
.
答:甲种笔记本销售了65本,则乙种笔记本销售了35本;
(2)不可能.理由如下:
设甲种笔记本销售了![]() 本,则乙种笔记本销售了
本,则乙种笔记本销售了![]() 本.若销售款为660,则有,
本.若销售款为660,则有,
![]() ,
,
解得![]() .
.
因销售本数应为整数,故所得销售款不可能是660元.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
元且期间,我市各大商场掀起购物狂湖,现有甲、乙、丙三个商场开展的促销活动如表所示:
商场 | 优惠活动 |
甲 | 全场按标价的 |
乙 | 实行“满 (如:顾客购衣服 |
丙 | 实行“满 |
根据以上活动信息,解决以下问题:
(1)三个 商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
(2)黄 先生发现在甲、乙商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
(3)丙商场又推出 “先打折”,“再满![]() 减
减![]() 元”的活动,张先生买了一件标价为
元”的活动,张先生买了一件标价为![]() 元的上衣,张先生发现竟然比没打折前多付了
元的上衣,张先生发现竟然比没打折前多付了![]() 元钱,问丙商场先打了多少折后再参加活动?
元钱,问丙商场先打了多少折后再参加活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
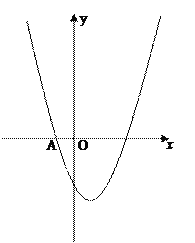
【题目】已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0).
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.
① 当点P' 落在该抛物线上时,求m的值;
② 当点P' 落在第二象限内,P'A2取得最小值时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
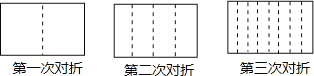
【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线):继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折n次,可以得到___________条折痕.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乔亚萍做一道数学题,“已知两个多项式![]()
![]() ,
,![]() ,试求
,试求![]() .”其中多项式
.”其中多项式![]() 的二次项系数印刷不清楚
的二次项系数印刷不清楚
(1)乔亚萍看了答案以后知道![]() ,请你替乔亚萍求出多项式
,请你替乔亚萍求出多项式![]() 的二次项系数;
的二次项系数;
(2)在(1)的基础上,乔亚萍已经将多项式![]() 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式![]() ,要求乔亚萍求出
,要求乔亚萍求出![]() 的结果.乔亚萍在求解时,误把“
的结果.乔亚萍在求解时,误把“![]() ”看成“
”看成“![]() ”,结果求出的答案为
”,结果求出的答案为![]() ,请你替乔亚萍求出“
,请你替乔亚萍求出“![]() ”的正确答案.
”的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售樱桃,已知樱桃的进价为15元/千克,如果售价为20元/千克,那么每天可售出250千克,如果售价为25元/千克,那么每天可售出200千克,经调查发现:每天的销售量y(千克)与售价x(元/千克)之间 存在一次函数关系.
(1)求y与x之间的函数关系式;
(2)若该超市每天要获得利润810元,同时又要让消费者得到实惠,则售价x应定于多少元?
(3)若樱桃的售价不得高于28元/千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是![]() 。
。

已知点A是数轴上的点,完成下列各题:
(1)如果点A表示的数是3,将点A先向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________;
(2)如果点A表示的数是-4,将点A先向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________;
(3)一般地,如果点A表示的数是m,将点A先向右移动n个单位长度,再向左移动t个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b是-5的相反数,c=-|-2|,且a、b、c分别是点A、B、C在数轴上对应的数.
![]()
(1)求a、b、c的值,并在数轴上标出点A、B、C.
(2)若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点P可以追上点Q?
(3)在数轴上找一点M,使点M到A、B、C三点的距离之和等于12,请求出所有点M对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
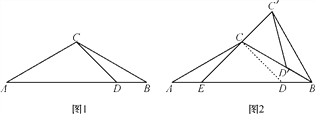
【题目】如图1,△ABC中,AC=BC,∠A=30°,点D在AB边上,且∠ADC=45°.
(1)求∠BCD的度数;
(2)将图1中的△BCD绕点B顺时针旋转得到△BC′D′,当点D′恰好落在BC边上时,如图2所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com