
����Ŀ��ij��������ӣ�ң���֪ӣ�ҵĽ���Ϊ15Ԫ/ǧ�ˣ�����ۼ�Ϊ20Ԫ/ǧ�ˣ���ôÿ����۳�250ǧ�ˣ�����ۼ�Ϊ25Ԫ/ǧ�ˣ���ôÿ����۳�200ǧ�ˣ������鷢�֣�ÿ���������y��ǧ�ˣ����ۼ�x��Ԫ/ǧ�ˣ�֮�� ����һ�κ�����ϵ��
��1����y��x֮��ĺ�����ϵʽ��
��2�����ó���ÿ��Ҫ�������810Ԫ��ͬʱ��Ҫ�������ߵõ�ʵ�ݣ����ۼ�xӦ���ڶ���Ԫ��
��3����ӣ�ҵ��ۼ۲��ø���28Ԫ/ǧ�ˣ������ۼ۶�Ϊ����ʱ���ó���ÿ������ӣ����������������������Ƕ���Ԫ��
���𰸡���1��y��x�ĺ�����ϵʽΪ��y=��10x+450����2���ó���ÿ��Ҫ�������810Ԫ��ͬʱ��Ҫ�������ߵõ�ʵ�ݣ����ۼ�xӦ����18Ԫ����3���ۼ�Ϊ28Ԫʱ��ÿ��������Ϊ2210Ԫ��
�������������������1��ֱ�����ô���ϵ�������һ�κ�������ʽ�����ó�����
��2��������������=������������������з�������������Ҫ�������ߵõ�ʵ�ݿɵô���
��3�����ȱ�ʾ��ÿ��Ļ��������������䷽����϶��κ��������Եó��𰸣�
���������������1����y��x�ĺ�����ϵʽΪ��y=kx+b���ѣ�20��250������25��200���������
![]() �������
������� ![]() ����y��x�ĺ�����ϵʽΪ��y=��10x+450��
����y��x�ĺ�����ϵʽΪ��y=��10x+450��
��2����������֪����x��15������10x+450��=810����������x2��60x+756=0��
�����x=42��x=18����Ҫ�������ߵõ�ʵ������x=18��
�����ó���ÿ��Ҫ�������810Ԫ��ͬʱ��Ҫ�������ߵõ�ʵ�������ۼ�xӦ����18Ԫ��
��3����ÿ�����WԪ��W=��x��15������10x+450��=��10x2+600x��6750=��10��x��30��2+2250��
��a=��10��0������������߶Գ���Ϊx=30������x��28ʱ��W��x���������������x=28ʱ��W���ֵ=13��170=2210��Ԫ����
�����ۼ�Ϊ28Ԫʱ��ÿ��������Ϊ2210Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������¶���:�����������ȵ�������a��b�����ʽa-b=ab.��ô��a��b������������������������(a��b).�磺��Ϊ![]() ��
��![]() .��������(3��
.��������(3��![]() )������������������.
)������������������.
(1)�����Ԣ�(1��![]() )����(-1��0)����(
)����(-1��0)����(![]() ��
��![]() )�У�����������������������____________(ֻ�����)��
)�У�����������������������____________(ֻ�����)��
(2)��(m��n)����������������������(-m��-n)___________����������������(������������������)��
(3)���������������һ������������������������һ����������5������һ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD=4����E�ڱ�AD�ϣ�����CE����CEΪ�������Ϸ���������CEFG����FH��AD������ΪH������AF��
(1)��֤��FH=ED��
(2)��AEΪ��ֵʱ����AEF��������
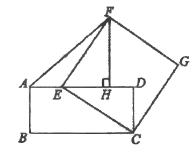
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ε�һ���ڽǵ�ƽ���߰Ѿ��ε�һ�߷ֳ���![]()
![]() ��
��![]()
![]() �������֣���ô���εĽ϶̱߳�Ϊ�� ��
�������֣���ô���εĽ϶̱߳�Ϊ�� ��
A. ![]()
![]() B.
B. ![]()
![]() C.
C. ![]()
![]() ��
��![]()
![]() D. ���϶�����
D. ���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľߵ꣬���ֱʼDZ����ÿ��8Ԫ�����ֱʼDZ����ÿ��5Ԫ�����죬�ס������ֱʼDZ��ϼ�����100����������695Ԫ!
��1�����ֱʼDZ��������˶��٣�
��2���������ۿ������660Ԫ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ΰ���ͼ��ʾ�Ĺ���ƴͼ�������еڢٸ�ͼ������1�������Σ��ڢڸ�ͼ������4�������Σ��ڢ۸�ͼ������8�������Σ��������˹���������ȥ����ڢ߸�ͼ���������εĸ���Ϊ��������

A. 15B. 17C. 19D. 24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С������һ�����AB�ĸ߶ȣ���֪С�����۾������ľ���EC=1.5�ף���һ�β�����C�͵ڶ��β�����D֮��ľ���CD=10�ף���AEG=30������AFG=60���������С������������˵ĸ߶ȣ�������������ţ�
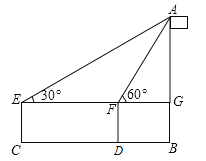
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɸ�����ͨ��ط��������ǵij��У��ס��������������450ǧ�ף��ӿ������г������г���ʻʱ���ԭ�ؿ��г���ʻʱ��������3Сʱ����֪�����г�ƽ����ʻ�ٶ���ԭ�ؿ��г�ƽ����ʻ�ٶȵ�3����������г���ƽ����ʻ�ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������Ƴ�һ���ɱ���λ500Ԫ/�˵�ʡ��������·���ο�����y����/�£������α���x��Ԫ/�ˣ�֮��Ĺ�ϵΪy=��x+1300����֪���������ܲ��Ź涨��������·������800Ԫ/�ˡ�1200Ԫ/��֮�䣮
��1��Ҫ����������·ÿ���ο�����������200�����ڣ����������·���۵�ȡֵ��Χ��
��2����Ӫ����������·ÿ������Ҫ����ͳɱ���
��3��������������·�����α���Ϊ����ʱ���ɻ�����������������Ƕ��٣�
���𰸡���1��ȡֵ��ΧΪ1100Ԫ/�ˡ�1200Ԫ/��֮�䣻��2��50000����3��x=900ʱ��w���=160000
�������������������1�����������в���ʽ���ɣ�
��2�����ݱ��ۼ�ȥ�ɱ��ɵõ������Ľ���ʽ������һ�κ�����ͼ����⼴�ɣ�
��3��������������˴γ��Լ۸ɵõ������Ľ���ʽ��Ȼ����ݶ��κ�������ֵ��⼴��.
�����������1�����������![]() ʱ����
ʱ����![]() ��
��
����![]()
��Ҫ����������·ÿ���ο�����������200�����ڣ���������·���۵�ȡֵ��ΧΪ1100Ԫ/��~1200Ԫ/��֮�䣻
��2��![]() ��
��![]() ����
����![]()
��![]() ���൱
���൱![]() ʱ��z��ͣ���
ʱ��z��ͣ���![]() ��
��
��3������![]()
��![]() ʱ��
ʱ��![]() .
.
�����͡������
��������
23
����Ŀ����֪�ı���ABCD�У�AB=AD���Խ���ACƽ�֡�DAB������C��CE��AB�ڵ�E����FΪAB��һ�㣬��EF=EB������DF��
��1����֤��CD=CF��
��2������DF����AC�ڵ�G����֤����DGC����ADC��
��3������HΪ�߶�DG��һ�㣬����AH������ADC=2��HAG��AD=3��DC=2����![]() ��ֵ��
��ֵ��
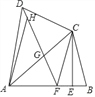
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com