
【题目】给出如下定义:如果两个不相等的有理数a,b满足等式a-b=ab.那么称a,b是“关联有理数对”,记作(a,b).如:因为![]() ,
,![]() .所以数对(3,
.所以数对(3,![]() )是“关联有理数对”.
)是“关联有理数对”.
(1)在数对①(1,![]() )、②(-1,0)、③(
)、②(-1,0)、③(![]() ,
,![]() )中,是“关联有理数对”的是____________(只填序号);
)中,是“关联有理数对”的是____________(只填序号);
(2)若(m,n)是“关联有理数对”,则(-m,-n)___________“关联有理数对”(填“是”或“不是”);
(3)如果两个有理数是一对“关联有理数对”,其中一个有理数是5,求另一个有理数.
【答案】(1)①③;(2)不是;(3)![]() 或
或![]() .
.
【解析】
(1)根据“关联有理数对”的定义逐个判断即可;
(2)根据(m,n)是“关联有理数对”可得m-n=mn,然后根据“关联有理数对”的定义判断(-m,-n)即可;
(3)设另一个有理数是x,分类讨论,根据“关联有理数对”的定义分别列方程求解即可.
解:(1)∵![]() ,
,![]() ,∴①(1,
,∴①(1,![]() )是“关联有理数对”,
)是“关联有理数对”,
∵-1-0=-1,-1×0=0,∴②(-1,0)不是“关联有理数对”,
∵![]() ,
,![]() ,∴③(
,∴③(![]() ,
,![]() )是“关联有理数对”,
)是“关联有理数对”,
故答案为:①③;
(2)∵(m,n)是“关联有理数对”,
∴m-n=mn,
而-m-(-n)=n-m,-m×(-n)=mn,
∴(-m,-n)不是“关联有理数对”,
故答案为:不是;
(3)设另一个有理数是x,
当(x,5)是“关联有理数对”时,则x-5=5x,
解得:![]() ,
,
当(5,x)是“关联有理数对”时,则5-x=5x,
解得:![]() ,
,
故另一个有理数是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
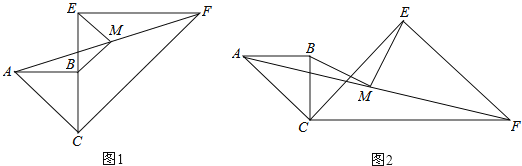
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
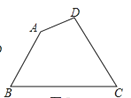
【题目】如图,现有一块四边形的木板余料ABCD,经测量AB=25cm,BC=54cm,CD=30cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
元且期间,我市各大商场掀起购物狂湖,现有甲、乙、丙三个商场开展的促销活动如表所示:
商场 | 优惠活动 |
甲 | 全场按标价的 |
乙 | 实行“满 (如:顾客购衣服 |
丙 | 实行“满 |
根据以上活动信息,解决以下问题:
(1)三个 商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
(2)黄 先生发现在甲、乙商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
(3)丙商场又推出 “先打折”,“再满![]() 减
减![]() 元”的活动,张先生买了一件标价为
元”的活动,张先生买了一件标价为![]() 元的上衣,张先生发现竟然比没打折前多付了
元的上衣,张先生发现竟然比没打折前多付了![]() 元钱,问丙商场先打了多少折后再参加活动?
元钱,问丙商场先打了多少折后再参加活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
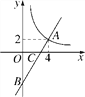
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6.
的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6.
(1)求函数y=![]() 和y=kx+b的解析式;
和y=kx+b的解析式;
(2)已知直线AB与x轴相交于点C,在第一象限内,求反比例函数y=![]() 的图象上一点P,使得S△POC=9.
的图象上一点P,使得S△POC=9.
查看答案和解析>>
科目:初中数学 来源: 题型:
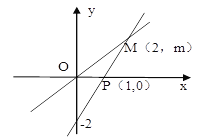
【题目】如图,一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M,
(1)求正比例函数和一次函数的解析式;
(2)根据图像写出使正比例函数的值大于一次函数的值的x的取值范围;
(3)求ΔMOP的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
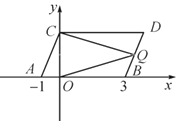
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.
(1)写出点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;
(3)点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个正确,请你找出这个结论并求值.
的值不变,其中有且只有一个正确,请你找出这个结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售樱桃,已知樱桃的进价为15元/千克,如果售价为20元/千克,那么每天可售出250千克,如果售价为25元/千克,那么每天可售出200千克,经调查发现:每天的销售量y(千克)与售价x(元/千克)之间 存在一次函数关系.
(1)求y与x之间的函数关系式;
(2)若该超市每天要获得利润810元,同时又要让消费者得到实惠,则售价x应定于多少元?
(3)若樱桃的售价不得高于28元/千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com