
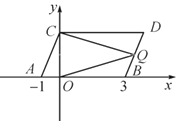
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.
(1)写出点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;
(3)点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个正确,请你找出这个结论并求值.
的值不变,其中有且只有一个正确,请你找出这个结论并求值.
【答案】(1)C(0,2),D(4,2),S四边形ABCD=8;(2)存在,点P的坐标为(0,4)或(0,-4);(3)结论①正确,![]() =1.
=1.
【解析】
(1)根据点平移的规律:左减右加,上加下减,即可得到点C、D的坐标,利用平行四边形的面积公式计算面积即可;
(2)设点P的坐标为(0,y),根据三角形的面积公式底乘以高的一半列式计算即可得到答案;
(3)结论①正确.过点Q作QE∥AB,交CO于点E,利用平行线的性质:两直线平行内错角相等证得∠DCQ+∠BOQ=∠CQO,由此得到结论①正确
(1)∵将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,
∴C(0,2),D(4,2),AB∥CD且AB=CD=4,
∴四边形ABDC是平行四边形,
∴S四边形ABCD=4×2=8.
(2)存在,
设点P的坐标为(0,y),根据题意,得![]() ×4×|y|=8.
×4×|y|=8.
解得y=4或y=-4.
∴点P的坐标为(0,4)或(0,-4).
(3)结论①正确.
过点Q作QE∥AB,交CO于点E.
∵AB∥CD,
∴QE∥CD.
∴∠DCQ=∠EQC,∠BOQ=∠EQO.
∵∠EQC+∠EQO=∠CQO,
∴∠DCQ+∠BOQ=∠CQO.
∴![]() =1.
=1.



科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律:
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
![]()
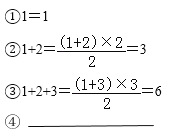
(2)通过猜想,写出(1)中与第八个点阵相对应的等式 ;
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的横线上写出相应的等式.


(4)通过猜想,写出(3)中与第n个点阵相对应的等式 ;
(5)判断256是不是正方形数,如果不是,说明理由;如果是,256可以看作哪两个相邻的“三角形数”之和?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出如下定义:如果两个不相等的有理数a,b满足等式a-b=ab.那么称a,b是“关联有理数对”,记作(a,b).如:因为![]() ,
,![]() .所以数对(3,
.所以数对(3,![]() )是“关联有理数对”.
)是“关联有理数对”.
(1)在数对①(1,![]() )、②(-1,0)、③(
)、②(-1,0)、③(![]() ,
,![]() )中,是“关联有理数对”的是____________(只填序号);
)中,是“关联有理数对”的是____________(只填序号);
(2)若(m,n)是“关联有理数对”,则(-m,-n)___________“关联有理数对”(填“是”或“不是”);
(3)如果两个有理数是一对“关联有理数对”,其中一个有理数是5,求另一个有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2017年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车?
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知A型车的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆.根据销售经验,A型车不少于B型车的2倍,但不超过B型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
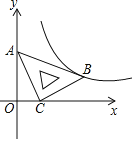
【题目】在平面直角坐标系![]() 中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标(1,0),顶点A的坐标为(0, 2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点
中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标(1,0),顶点A的坐标为(0, 2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点![]() 的坐标为__________
的坐标为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
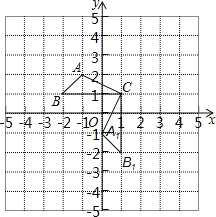
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点__逆时针旋转__度得到的,B1的坐标是__;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
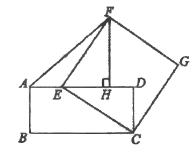
【题目】如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)当AE为何值时,△AEF的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贵成高铁开通后极大地方便了人们的出行,甲、乙两个城市相距450千米,加开高铁列车后,高铁列车行驶时间比原特快列车行驶时间缩短了3小时,已知高铁列车平均行驶速度是原特快列车平均行驶速度的3倍,求高铁列车的平均行驶速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com