练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如果矩形的一个内角的平分线把矩形的一边分成了和的两部分，那么矩形的较短边长为（ ）

    A. B. C. 或D. 以上都不对

    【答案】C

    【解析】

    利用角平分线得到∠ABE=∠CBE，矩形对边平行得到∠AEB=∠CBE．那么可得到∠ABE=∠AEB，可得到AB=AE．那么根据AE的不同情况得到矩形各边长，进而求得周长．

    解：如图：

    ∵矩形ABCD中BE是角平分线．
    ∴∠ABE=∠EBC．
    ∵AD∥BC．
    ∴∠AEB=∠EBC．
    ∴∠AEB=∠ABE．
    ∴AB=AE．
    平分线把矩形的一边分成3cm和5cm．
    当AE=3cm时：则AB=CD=3cm，AD=CB=8cm则矩形的较短边是：3cm；
    当AE=5cm时：AB=CD=5cm，AD=CB=8cm，则矩形的较短边是：5cm．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

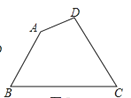
    【题目】如图，现有一块四边形的木板余料ABCD，经测量AB=25cm，BC=54cm，CD=30cm，且tanB=tanC=，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，则该矩形的面积为____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

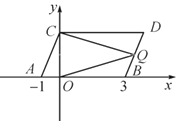
    【题目】如图，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，分别得到点A，B的对应点C，D.连接AC，BD.

    (1)写出点C，D的坐标及四边形ABDC的面积.

    (2)在y轴上是否存在一点P，连接PA，PB，使S三角形PAB＝S四边形ABDC？若存在，求出点P的坐标，若不存在，试说明理由；

    (3)点Q是线段BD上的动点，连接QC，QO，当点Q在BD上移动时(不与B，D重合)，给出下列结论：①的值不变；②的值不变，其中有且只有一个正确，请你找出这个结论并求值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC.

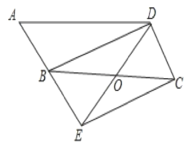
    (1)求证：四边形BECD是平行四边形；

    (2)若∠A=50°,则当∠BOD=___°时，四边形BECD是矩形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一张长方形的纸对折，如图所示可得到一条折痕（图中虚线）：继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么对折n次，可以得到___________条折痕.

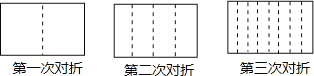
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0 ②4a+2b+c＞0 ③4ac﹣b2＜8a ④＜a＜⑤b＞c．其中含所有正确结论的选项是（　　）

    A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市销售樱桃，已知樱桃的进价为15元/千克，如果售价为20元/千克，那么每天可售出250千克，如果售价为25元/千克，那么每天可售出200千克，经调查发现：每天的销售量y（千克）与售价x（元/千克）之间 存在一次函数关系．

    （1）求y与x之间的函数关系式；

    （2）若该超市每天要获得利润810元，同时又要让消费者得到实惠，则售价x应定于多少元？

    （3）若樱桃的售价不得高于28元/千克，请问售价定为多少时，该超市每天销售樱桃所获的利润最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知张强家、体育场、文具店在同一直线上，下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家．图中表示时间，表示张强离家的距离．

    根据图象解答下列问题：

    （1）体育场离张强家多远？张强从家到体育场用了多少时间？

    （2）体育场离文具店多远？

    （3）张强在文具店停留了多少时间？

    （4）求张强从文具店回家过程中与的函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

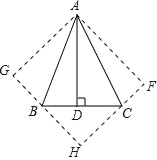
    【题目】如图，在△ABC中，∠BAC=45°，AD⊥BC于D，将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H．

    （1）求证：四边形AFHG为正方形；

    （2）若BD=6，CD=4，求AB的长．

    查看答案和解析>>

    同步练习册答案