
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
【答案】D
【解析】试题分析:①∵函数开口方向向上,∴a>0;∵对称轴在y轴右侧,∴ab异号,∵抛物线与y轴交点在y轴负半轴,∴c<0,∴abc>0,故①正确;②∵图象与x轴交于点A(﹣1,0),对称轴为直线x=1,∴图象与x轴的另一个交点为(3,0),∴当x=2时,y<0,∴4a+2b+c<0,故②错误;③∵图象与x轴交于点A(﹣1,0),∴当x=﹣1时,y= ![]() =0,∴a﹣b+c=0,即a=b﹣c,c=b﹣a,∵对称轴为直线x=1,∴
=0,∴a﹣b+c=0,即a=b﹣c,c=b﹣a,∵对称轴为直线x=1,∴![]() =1,即b=﹣2a,∴c=b﹣a=(﹣2a)﹣a=﹣3a,∴4ac﹣
=1,即b=﹣2a,∴c=b﹣a=(﹣2a)﹣a=﹣3a,∴4ac﹣![]() =4a(﹣3a)﹣
=4a(﹣3a)﹣![]() =
=![]() <0,∵8a>0,∴4ac﹣
<0,∵8a>0,∴4ac﹣![]() <8a,故③正确;④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,∴﹣2<c<﹣1,∴﹣2<﹣3a<﹣1,∴
<8a,故③正确;④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,∴﹣2<c<﹣1,∴﹣2<﹣3a<﹣1,∴![]() >a>
>a>![]() ,故④正确;⑤∵a>0,∴b﹣c>0,即b>c,故⑤正确.
,故④正确;⑤∵a>0,∴b﹣c>0,即b>c,故⑤正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】综合与实践
阅读以下材料:
定义:两边分别相等且夹角互补的两个三角形叫做“互补三角形”.
用符号语言表示为:如图①,在△ABC与△DEF中,如果AC=DE,∠C+∠E=180°,BC=EF,那么△ABC与△DEF是互补三角形.
反之,“如果△ABC与△DEF是互补三角形,那么有AC=DE,∠C+∠E=180°,BC=EF”也是成立的.
自主探究
利用上面所学知识以及全等三角形的相关知识解决问题:
(1)性质:互补三角形的面积相等
如图②,已知△ABC与△DEF是互补三角形.
求证:△ABC与△DEF的面积相等.
证明:分别作△ABC与△DEF的边BC,EF上的高线,则∠AGC=∠DHE=90°.
…… (将剩余证明过程补充完整)
(2)互补三角形一定不全等,请你判断该说法是否正确,并说明理由,如果不正确,请举出一个反例,画出示意图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=xm.

(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD、AD的距离分别是13m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系![]() 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线![]() 经过点
经过点![]() 、
、![]() ,点
,点![]() 是第一象限的点且
是第一象限的点且![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() .
.

(1)求直线![]() 的解析式和点
的解析式和点![]() 的坐标;
的坐标;
(2)试说明:![]() ;
;
(3)若点![]() 是直线
是直线![]() 上的一个动点,在
上的一个动点,在![]() 轴上存在另一个点
轴上存在另一个点![]() ,且以
,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请直接写出点
为顶点的四边形是平行四边形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
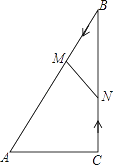
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发, 在
出发, 在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,设运动时间为
匀速运动,设运动时间为![]() 秒
秒![]() ,连接
,连接![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 的面积为
的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对称轴平行于y轴的抛物线过点A(1,0)、B(3,0)和C(4,6);
(1)求抛物线的表达式;
(2)现将此抛物线先沿x轴方向向右平移6个单位,再沿y轴方向平移k个单位,若所得抛物线与x轴交于点D、E(点D在点E的左边),且使△ACD∽△AEC(顶点A、C、D依次对应顶点A、E、C),试求k的值,并注明方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读一读:式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可以将“1+2+3+4+5+…+100”表示为![]() ,这里“
,这里“![]() ”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为
”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为![]() (2n-1);又如13+23+33+43+53+63+73+83+93+103可表示为
(2n-1);又如13+23+33+43+53+63+73+83+93+103可表示为![]() n3.
n3.
通过对上以材料的阅读,请解答下列问题.
(1)2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符合可表示为_________________;
(2)计算![]() (n2-1)=________________.(填写最后的计算结果)
(n2-1)=________________.(填写最后的计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】气象台发布的卫星云图显示,代号为![]() 的台风在某海岛(设为点
的台风在某海岛(设为点![]() )的南偏东
)的南偏东![]() 方向的
方向的![]() 点生成,测得
点生成,测得![]() .台风中心从点
.台风中心从点![]() 以
以![]() 的速度向正北方向移动,经
的速度向正北方向移动,经![]() 后到达海面上的点
后到达海面上的点![]() 处.因受气旋影响,台风中心从点
处.因受气旋影响,台风中心从点![]() 开始以
开始以![]() 的速度向北偏西
的速度向北偏西![]() 方向继续移动.以
方向继续移动.以![]() 为原点建立如图所示的直角坐标系.
为原点建立如图所示的直角坐标系.
(1)台风中心生成点![]() 的坐标为 ,台风中心转折点
的坐标为 ,台风中心转折点![]() 的坐标为 ;(结果保留根号)
的坐标为 ;(结果保留根号)
(2)已知距台风中心![]() 范围内均会受到台风侵袭.如果某城市(设为点
范围内均会受到台风侵袭.如果某城市(设为点![]() )位于点
)位于点![]() 的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com