
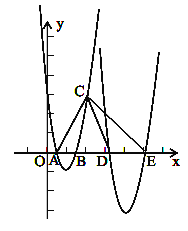
【题目】平面直角坐标系xOy中,对称轴平行于y轴的抛物线过点A(1,0)、B(3,0)和C(4,6);
(1)求抛物线的表达式;
(2)现将此抛物线先沿x轴方向向右平移6个单位,再沿y轴方向平移k个单位,若所得抛物线与x轴交于点D、E(点D在点E的左边),且使△ACD∽△AEC(顶点A、C、D依次对应顶点A、E、C),试求k的值,并注明方向.

【答案】(1)y=2x2﹣8x+6;(2)向下平移6个单位.
【解析】试题分析:(1)利用待定系数法直接求出抛物线的解析式;
(2)设出D,E坐标,根据平移,用k表示出平移后的抛物线解析式,利用坐标轴上点的特点得出m+n=16,mn=63﹣![]() ,进而利用相似三角形得出比例式建立方程即可求出k.
,进而利用相似三角形得出比例式建立方程即可求出k.
试题解析:解:(1)∵抛物线过点A(1,0)、B(3,0),∴设抛物线的解析式为y=a(x﹣1)(x﹣3)。
∵C(4,6),∴6=a(4﹣1)(4﹣3),∴a=2,∴抛物线的解析式为y=2(x﹣1)(x﹣3)=2x2﹣8x+6;
(2)如图,设点D(m,0),E(n,0)。
∵A(1,0),∴AD=m﹣1,AE=n﹣1。
由(1)知,抛物线的解析式为y=2x2﹣8x+6=2(x﹣2)2﹣2,∴将此抛物线先沿x轴方向向右平移6个单位,得到抛物线的解析式为y=2(x﹣8)2﹣2,∴再沿y轴方向平移k个单位,得到的抛物线的解析式为y=2(x﹣8)2﹣2﹣k。
令y=0,则2(x﹣8)2﹣2﹣k=0,∴2x2﹣32x+126﹣k=0。
根据根与系数的关系得:∴m+n=16,mn=63﹣![]() 。
。
∵A(1,0),C(4,6),∴AC2=(4﹣1)2+62=45。
∵△ACD∽△AEC,∴ ![]() ,∴AC2=ADAE,∴45=(m﹣1)(n﹣1)=mn﹣(m+n)+1,
,∴AC2=ADAE,∴45=(m﹣1)(n﹣1)=mn﹣(m+n)+1,
∴45=63﹣![]() ﹣16+1,∴k=6,即:k=6,向下平移6个单位.
﹣16+1,∴k=6,即:k=6,向下平移6个单位.


科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:
(1)点A、B、C分别表示的数是______________________。
(2)将点B 向右移动三个单位长度后到达点D,点D表示的数是_____________。
(3)移动点A到达点E,使B、C、E三点的其中任意一点为连接另外两点之间线段的中点,请直接写出所有点A 移动的距离和方向。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=8cm,对角线AC、BD相交于点O,点E、F分别从B、C两点同时出发,以1cm/s的速度沿BC、CD运动,到点C、D时停止运动,设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )


A. A B. B C. C D. D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2﹣4x+4沿y轴向下平移9个单位,所得新抛物线与x轴正半轴交于点B,与y轴交于点C,顶点为D.求:(1)点B、C、D坐标;(2)△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,点E是AC的一点,连接EB,过点A做AM⊥BE,垂足为M,AM与BD相交于点F.
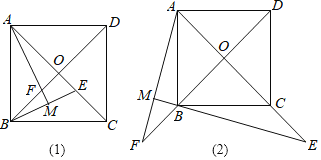
(1)猜想:如图(1)线段OE与线段OF的数量关系为 ;
(2)拓展:如图(2),若点E在AC的延长线上,AM⊥BE于点M,AM、DB的延长线相交于点F,其他条件不变,(1)的结论还成立吗?如果成立,请仅就图(2)给出证明;如果不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com