
【题目】计算:
(1)![]() ;
;
(2) ;
;
(3)![]() ;
;
(4)![]() .
.
(5)![]() ;
;
(6)
【答案】(1)15;(2)6;(3)3;(4)7;(5)2.32;(6)2.
【解析】
(1)先化简,再计算加减法即可求解;
(2)(5)(6)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;
(3)先算乘除,后算减法即可求解;
(4)根据乘法分配律简便计算.
(1)20+8(1)+(4)
=20+8+14
=24+9
=15;
(2)![]() ×(
×(![]() )2÷(0.5)3
)2÷(0.5)3
=![]()
=6;
(3)46÷(2)×(![]() )
)
=4+3×(![]() )
)
=41
=3;
(4)(36)×(![]() )
)
=36×![]()
=1624+15
=7;
(5)(2)2×0.5(1.6)2÷(2)3
=4×0.52.56÷(8)
=2+0.32
=2.32;
(6)14÷(4)(![]() )2×(3)+|(1)22|
)2×(3)+|(1)22|
=1÷(4)![]() ×(3)+|12|
×(3)+|12|
=![]() +
+![]() +1
+1
=2.


科目:初中数学 来源: 题型:
【题目】有理数 a、b、c 在数轴上对应的点的位置,如图所示:① abc<0;② |a-b|+|b-c|=|a-c|;③ (a-b)(b-c)(c-a)>0;④ |a|<1-bc,以上四个结论正确的有( )个
![]()
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线![]() 经过点
经过点![]() 、
、![]() ,点
,点![]() 是第一象限的点且
是第一象限的点且![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() .
.

(1)求直线![]() 的解析式和点
的解析式和点![]() 的坐标;
的坐标;
(2)试说明:![]() ;
;
(3)若点![]() 是直线
是直线![]() 上的一个动点,在
上的一个动点,在![]() 轴上存在另一个点
轴上存在另一个点![]() ,且以
,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请直接写出点
为顶点的四边形是平行四边形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对称轴平行于y轴的抛物线过点A(1,0)、B(3,0)和C(4,6);
(1)求抛物线的表达式;
(2)现将此抛物线先沿x轴方向向右平移6个单位,再沿y轴方向平移k个单位,若所得抛物线与x轴交于点D、E(点D在点E的左边),且使△ACD∽△AEC(顶点A、C、D依次对应顶点A、E、C),试求k的值,并注明方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几年前我国曾经流行有一种叫“二十四点”的数学趣味算题,方法是给出1~13之间的自然数,从中任取四个,将这四个数(四个数都只能用一次)进行“+”“-”“×”“÷”运算,可加括号使其结果等于24.
例如:对1,2,3,4可运算(1+2+3)×4=24,也可以写成4×(1+2+3)=24,但视作相同的方法.
现有郑、付两同学的手中分别握着四张扑克牌(见下图);若红桃、方块上的点数记为负数,黑桃、梅花上的点数记为正数.
请你对郑、付两同学的扑克牌的按要求进行记数,并按前面“二十四点”运算方式对郑、付两同学的记数分别进行列式计算,使其运算结果均为24.(分别尽可能提供多种算法)

依次记为:______ 、______ 、______ 、______

依次记为:______ 、______ 、______ 、______ .
(1)帮助郑同学列式计算:______
(2)帮助付同学列式计算:______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读一读:式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可以将“1+2+3+4+5+…+100”表示为![]() ,这里“
,这里“![]() ”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为
”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为![]() (2n-1);又如13+23+33+43+53+63+73+83+93+103可表示为
(2n-1);又如13+23+33+43+53+63+73+83+93+103可表示为![]() n3.
n3.
通过对上以材料的阅读,请解答下列问题.
(1)2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符合可表示为_________________;
(2)计算![]() (n2-1)=________________.(填写最后的计算结果)
(n2-1)=________________.(填写最后的计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
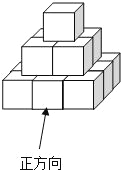
【题目】把棱长为1cm的若干个小正方体摆放如图所示的几何体,然后在露出的表面上涂上颜色![]() 不含底面
不含底面![]()
![]() 该几何体中有多少小正方体?
该几何体中有多少小正方体?
![]() 画出主视图.
画出主视图.
![]() 求出涂上颜色部分的总面积.
求出涂上颜色部分的总面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
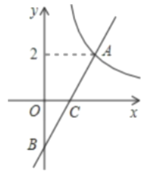
【题目】如图在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象的交点为
的图象的交点为![]() .
.
(1)求一次函数的解析式;
(2)设一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,若点
,若点![]() 是
是![]() 轴上一点,且满足
轴上一点,且满足![]() 的面积是6,求点
的面积是6,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com