
【题目】如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:
(1)点A、B、C分别表示的数是______________________。
(2)将点B 向右移动三个单位长度后到达点D,点D表示的数是_____________。
(3)移动点A到达点E,使B、C、E三点的其中任意一点为连接另外两点之间线段的中点,请直接写出所有点A 移动的距离和方向。
![]()
【答案】(1)﹣4,﹣2,3;(2)1;(3)点A向右移动4.5个单位长度或12个单位长度,点A向左移动3个单位长度.
【解析】
(1)根据点A、B、C在数轴上的位置写出即可;
(2)将点B向右移动三个单位长度后到达点D,则点D表示的数为-2+3=1;
(3)分类讨论:当点A向左移动时,则点B为线段AC的中点;当点A向右移动并且落在BC之间,则A点为BC的中点;当点A向右移动并且在线段BC的延长线上,则C点为BA的中点,然后根据中点的定义分别求出对应的A点表示的数,从而得到移动的距离.
解:(1)点A、B、C分别表示的数分别是﹣4,﹣2,3;
(2)将点B 向右移动三个单位长度后到达点D,点D表示的数是1;
(3)当点A向左移动时,则点B为线段AC的中点,
∵线段BC=3-(-2)=5,
∴点A距离点B有5个单位,
∴点A要向左移动3个单位长度;
当点A向右移动并且落在BC之间,则A点为BC的中点,
∴A点在B点右侧,距离B点2.5个单位,
∴点A要向右移动4.5单位长度;
当点A向右移动并且在线段BC的延长线上,则C点为BA的中点,
∴点A要向右移动12个单位长度.
故答案为:(1)﹣4,﹣2,3;(2)1;(3)点A向右移动4.5个单位长度或12个单位长度,点A向左移动3个单位长度.


科目:初中数学 来源: 题型:
【题目】直角坐标系中,已知点P(-2,-1),点T(t,0)是x轴上的一个动点.

(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B、C、D在数轴上的位置如图1所示,已知AB=3,BC=2,CD=4.
(1)若点C为原点,则点A表示的数是 ;
(2)若点A、B、C、D分别表示有理数a,b,c,d,则|a﹣c|+|d﹣b|﹣|a﹣d|= ;
(3)如图2,点P、Q分别从A、D两点同时出发,点P沿线段AB以每秒1个单位长度的速度向右运动,到达B点后立即按原速折返;点Q沿线段CD以每秒2个单位长度的速度向左运动,到达C点后立即按原速折返.当P、Q中的某点回到出发点时,两点同时停止运动.
①当点停止运动时,求点P、Q之间的距离;
②设运动时间为t(单位:秒),则t为何值时,PQ=5?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
阅读以下材料:
定义:两边分别相等且夹角互补的两个三角形叫做“互补三角形”.
用符号语言表示为:如图①,在△ABC与△DEF中,如果AC=DE,∠C+∠E=180°,BC=EF,那么△ABC与△DEF是互补三角形.
反之,“如果△ABC与△DEF是互补三角形,那么有AC=DE,∠C+∠E=180°,BC=EF”也是成立的.
自主探究
利用上面所学知识以及全等三角形的相关知识解决问题:
(1)性质:互补三角形的面积相等
如图②,已知△ABC与△DEF是互补三角形.
求证:△ABC与△DEF的面积相等.
证明:分别作△ABC与△DEF的边BC,EF上的高线,则∠AGC=∠DHE=90°.
…… (将剩余证明过程补充完整)
(2)互补三角形一定不全等,请你判断该说法是否正确,并说明理由,如果不正确,请举出一个反例,画出示意图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请用两种不同的方法列代数式表示图1的面积
方法1 ,
方法2 ;
(2)若a+b=7,ab=15,根据(1)的结论求a2+b2的值;
(3)如图2,将边长为x和x+2的长方形,分成边长为x的正方形和两个宽为1的小长方形,并将这三个图形拼成图3,这时只需要补一个边长为1的正方形便可以构成一个大正方形.
①若一个长方形的面积是216,且长比宽大6,求这个长方形的宽.
②把一个长为m,宽为n的长方形(m>n)按上述操作,拼成一个在一角去掉一个小正方形的大正方形,则去掉的小正方形的边长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
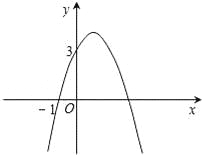
【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数 a、b、c 在数轴上对应的点的位置,如图所示:① abc<0;② |a-b|+|b-c|=|a-c|;③ (a-b)(b-c)(c-a)>0;④ |a|<1-bc,以上四个结论正确的有( )个
![]()
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=xm.

(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD、AD的距离分别是13m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对称轴平行于y轴的抛物线过点A(1,0)、B(3,0)和C(4,6);
(1)求抛物线的表达式;
(2)现将此抛物线先沿x轴方向向右平移6个单位,再沿y轴方向平移k个单位,若所得抛物线与x轴交于点D、E(点D在点E的左边),且使△ACD∽△AEC(顶点A、C、D依次对应顶点A、E、C),试求k的值,并注明方向.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com