
【题目】直角坐标系中,已知点P(-2,-1),点T(t,0)是x轴上的一个动点.

(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
【答案】(1)点P关于原点的对称点P′的坐标为(2,1);(2)综上所述,符合条件的t的值为-![]() ,
, ![]() ,
, ![]() ,4.
,4.
【解析】试题分析: (1)根据坐标关于原点对称的特点即可得出点P′的坐标,(2)要分类讨论,动点T在原点左侧和右侧时分别进行讨论即可得出当t取何值时,△P′TO是等腰三角形.
试题解析:(1) 点P关于原点的对称点P′的坐标为(2,1).
(2)OP′=![]() .
.
(a)动点T在原点左侧,
当T1O=P′O=![]() 时,△P′TO是等腰三角形,
时,△P′TO是等腰三角形,
∴点T1(-![]() ,0),.
,0),.
(b)动点T在原点右侧,
①当T2O=T2P′时,△P′TO是等腰三角形,得T2(![]() ,0),
,0),
②当T3O=P′O时,△P′TO是等腰三角形,得点T3(![]() ,0),
,0),
③当T4P′=P′O时,△P′TO是等腰三角形,得点T4(4,0).
综上所述,符合条件的t的值为-![]() ,
,![]() ,
,![]() ,4.
,4.


科目:初中数学 来源: 题型:
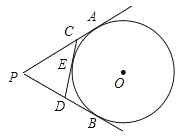
【题目】如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
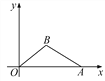
【题目】如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=![]() . 求:(1)点B的坐标;(2)cos∠BAO的值.
. 求:(1)点B的坐标;(2)cos∠BAO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张丘建,我国南北朝时期(约公元5世纪)著名的数学家,著有《张丘建算经》.一次宴会上,张丘建出了一道题:“现有一只鹿向西跑,当猎人追至![]() 处时,与鹿所在的
处时,与鹿所在的![]() 处还差36步(古代:1里=300步);鹿突然向北跑,此时骑马的猎人就沿着
处还差36步(古代:1里=300步);鹿突然向北跑,此时骑马的猎人就沿着![]() 追去,追了50步至
追去,追了50步至![]() 处与鹿所在的位置
处与鹿所在的位置![]() 处还差10步(点
处还差10步(点![]() 、
、![]() 、
、![]() 在同一直线上).如果此鹿不向北转,而继续向西跑,猎人需要追多远才能追上此鹿?”,已知单位时间内鹿跑的路程和猎人骑马追赶的路程的比值是定值,请解答这个问题.
在同一直线上).如果此鹿不向北转,而继续向西跑,猎人需要追多远才能追上此鹿?”,已知单位时间内鹿跑的路程和猎人骑马追赶的路程的比值是定值,请解答这个问题.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:
如图1,已知点![]() 是正方形
是正方形![]() 的两条对角线的交点,以点
的两条对角线的交点,以点![]() 为直角顶点的直角三角形
为直角顶点的直角三角形![]() 的两边
的两边![]() ,
,![]() 分别过点
分别过点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.

(1)![]() 的长度为________;
的长度为________;
操作证明:
(2)如图2,在(1)的条件下,将![]() 按如图放置,若
按如图放置,若![]() ,
,![]() 分别与
分别与![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() .请判断
.请判断![]() 和
和![]() 有怎样的数量关系,并证明结论;
有怎样的数量关系,并证明结论;

探究发现:
(3)如图3,在(1)的条件下,将![]() 按如图放置,若点
按如图放置,若点![]() 恰好在
恰好在![]() 上,求证:
上,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
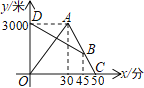
【题目】某天早晨,小童从家跑步去体育场锻炼,同时小郑从体育场晨练结束回家,途中两人相遇.小童跑到体育场后发现要下雨,立即按原路返回,遇到小郑后两人一起回到家(小童和小郑始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与小童出发的时间x(分)之间的函数图象.当x=_______时,小童与小郑相距600米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x 轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:
(1)点A、B、C分别表示的数是______________________。
(2)将点B 向右移动三个单位长度后到达点D,点D表示的数是_____________。
(3)移动点A到达点E,使B、C、E三点的其中任意一点为连接另外两点之间线段的中点,请直接写出所有点A 移动的距离和方向。
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com