
【题目】综合与实践
问题情境:
如图1,已知点![]() 是正方形
是正方形![]() 的两条对角线的交点,以点
的两条对角线的交点,以点![]() 为直角顶点的直角三角形
为直角顶点的直角三角形![]() 的两边
的两边![]() ,
,![]() 分别过点
分别过点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.

(1)![]() 的长度为________;
的长度为________;
操作证明:
(2)如图2,在(1)的条件下,将![]() 按如图放置,若
按如图放置,若![]() ,
,![]() 分别与
分别与![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() .请判断
.请判断![]() 和
和![]() 有怎样的数量关系,并证明结论;
有怎样的数量关系,并证明结论;

探究发现:
(3)如图3,在(1)的条件下,将![]() 按如图放置,若点
按如图放置,若点![]() 恰好在
恰好在![]() 上,求证:
上,求证:![]() .
.

【答案】(1)![]() ;(2)
;(2)![]() ,证明详见解析;(3)详见解析
,证明详见解析;(3)详见解析
【解析】
(1)由题意可得OC=OB,OC⊥OB,再根据勾股定理即可得到答案;
(2)连接![]() ,
,![]() ,证明
,证明![]() ,即可得出答案;
,即可得出答案;
(3)根据题意可推出![]() 为等边三角形,可得
为等边三角形,可得![]() ,
,![]() ,再根据
,再根据![]() ,可得
,可得![]() ,从而可推出,
,从而可推出,![]() ,即可得证.
,即可得证.
解:(1)∵点![]() 是正方形
是正方形![]() 的两条对角线的交点,以点
的两条对角线的交点,以点![]() 为直角顶点的直角三角形
为直角顶点的直角三角形![]() 的两边
的两边![]() ,
,![]() 分别过点
分别过点![]() ,C,
,C,
∴OC=OB,OC⊥OB,
∵BC=2,
∴OC2=BC2-OB2,
2OC2=BC2,
2OC2=4,
即OC=![]() ;
;
(2)![]() ;
;
证明:如图,连接![]() ,
,![]() ,
,

∵点![]() 是正方形
是正方形![]() 的两条对角线的交点,
的两条对角线的交点,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中 ,
,
∴![]() ,
,
∴![]() ;
;
(3)连接![]() ,
,![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我们规定:相等的实数看作同一个实数.有下列六种说法:
①数轴上有无数多个表示无理数的点;
②带根号的数不一定是无理数;
③每个有理数都可以用数轴上唯一的点来表示;
④数轴上每一个点都表示唯一一个实数;
⑤没有最大的负实数,但有最小的正实数;
⑥没有最大的正整数,但有最小的正整数.
其中说法错误的有_____(注:填写出所有错误说法的编号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店准备购进A、B两种型号的书包共50个进行销售,两种书包的进价、售价如下表所示:
书包型号 | 进价(元/个) | 售价(元/个) |
A型 | 200 | 300 |
B型 | 100 | 150 |
购进这50个书包的总费用不超过7300元,且购进B型书包的个数不大于A型书包个数的![]() .
.
(1)该文具店有哪几种进货方案?
(2)若该文具店购进的50个书包全部售完,则该文具店采用哪种进货方案,才能获得最大利润?最大利润是多少?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点O是对角线BD中点,点E在边BC上,EO的延长线与边AD交于点F,连接BF、DE,如图1.

(1)求证:四边形BEDF是平行四边形;
(2)在(1)中,若DE=DC,∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、R,如图2.
①当CD=6,CE=4时,求BE的长.
②探究BH与AF的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角坐标系中,已知点P(-2,-1),点T(t,0)是x轴上的一个动点.

(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,拦水坝的横断面为等腰梯形ABCD,坝顶宽BC为6 m,坝高为3.2 m,为了提高水坝的拦水能力需要将水坝加高2 m,并且保持坝顶宽度不变,迎水坡CD的坡度不变,但是背水坡的坡度由原来的1∶2变成1∶2.5(坡度是坡高与坡的水平长度的比).求加高后的坝底HD的长为多少.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,把4个长为a,宽为b的长方形拼成如图②所示的图形,且a=3b,则根据这个图形不能得到的等式是( )

A.(a+b)2=4ab+(a-b)2B.4b2+4ab=(a+b)2
C.(a-b)2=16b2-4abD.(a-b)2+12a2=(a+b)2
查看答案和解析>>
科目:初中数学 来源: 题型:
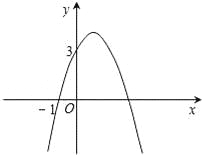
【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com