
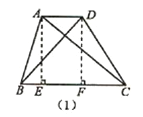
【题目】在平行四边形ABCD中,点O是对角线BD中点,点E在边BC上,EO的延长线与边AD交于点F,连接BF、DE,如图1.

(1)求证:四边形BEDF是平行四边形;
(2)在(1)中,若DE=DC,∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、R,如图2.
①当CD=6,CE=4时,求BE的长.
②探究BH与AF的数量关系,并给予证明.
【答案】(1)详见解析;(2)①4![]() ﹣2;②AF=
﹣2;②AF=![]() BH,详见解析
BH,详见解析
【解析】
(1)由“ASA”可得△BOE≌△DOF,可得DF=BE,可得结论;
(2)①由等腰三角形的性质可得EN=CN=2,由勾股定理可求DN,由等腰三角形的性质可求BN的长,即可求解;
②如图,过点H作HM⊥BC于点M,由“AAS”可证△HMC≌△CND,可得HM=CN,由等腰直角三角形的性质可得BH=![]() HM,即可得结论.
HM,即可得结论.
(1)证明:∵平行四边形ABCD中,点O是对角线BD中点,
∴AD∥BC,BO=DO,
∴∠ADB=∠CBD,且∠DOF=∠BOE,BO=DO,
∴△BOE≌△DOF(ASA)
∴DF=BE,且DF∥BE,
∴四边形BEDF是平行四边形;
(2)①如图2,过点D作DN⊥EC于点N,

∵DE=DC=6,DN⊥EC,
∴EN=CN=2,
∴DN=![]() =
=![]() =4
=4![]() ,
,
∵∠DBC=45°,DN⊥BC,
∴∠DBC=∠BDN=45°,
∴DN=BN=4![]() ,
,
∴BE=BN﹣EN=4﹣2![]() ;
;
故答案为:BE=4﹣2![]() .
.
②AF=![]() BH,
BH,
理由如下:如图,过点H作HM⊥BC于点M,

∵DN⊥EC,CG⊥DE,
∴∠CEG+∠ECG=90°,∠DEN+∠EDN=90°,
∴∠EDN=∠ECG,
∵DE=DC,DN⊥EC,
∴∠EDN=∠CDN,EC=2CN,
∴∠ECG=∠CDN,
∵∠DHC=∠DBC+∠BCH=45°+∠BCH,∠CDB=∠BDN+∠CDN=45°+∠CDN,
∴∠CDB=∠DHC,
∴CD=CH,且∠HMC=∠DNC=90°,∠ECG=∠CDN,
∴△HMC≌△CND(AAS)
∴HM=CN,
∵HM⊥BC,∠DBC=45°,
∴∠BHM=∠DBC=45°,
∴BM=HM,
∴BH=![]() HM,
HM,
∵AD=BC,DF=BE,
∴AF=EC=2CN,
∴AF=2HM=![]() BH.
BH.
故答案为:AF=![]() BH.
BH.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】说明:在解答“结论应用”时,从(A),(B)两题中仸选一题做答.
问题探究
启知学习小组在课外学习时,发现了这样一个问题:如图(1),在四边形ABCD中,连接AC,BD,如果△ABC与△BCD的面积相等,那么AD∥BC.在小组交流时,他们在图(1)中添加了如图所示的辅助线,AE⊥BC于点E,DF⊥BC于点F.请你完成他们的证明过程.
结论应用
在平面直角坐标系中,反比例函数![]() 的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
(A)(1)求反比例函数的表达式;
(2)如图(2),已知b=1,AC,BD相交于点E,求证:CD∥AB.
(B)(1)求反比例函数的表达式;
(2)如图(3),若点B在第三象限,判断并证明CD与AB的位置关系.
我选择:


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且OE⊥OF,则四边形AFOE的面积是( )

A.4B.2C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=![]() . 求:(1)点B的坐标;(2)cos∠BAO的值.
. 求:(1)点B的坐标;(2)cos∠BAO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学全体团员积极响应团委的号召,开展了“牵手儿童,奉献爱心”捐款活动.捐款活动结束后,某班班长将全班40名团员的捐款情况进行了统计,并绘制成如下的统计图.


(1)这40名团员捐款的中位数是________元,众数是________元;
(2)求这40名团员捐款的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:
如图1,已知点![]() 是正方形
是正方形![]() 的两条对角线的交点,以点
的两条对角线的交点,以点![]() 为直角顶点的直角三角形
为直角顶点的直角三角形![]() 的两边
的两边![]() ,
,![]() 分别过点
分别过点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.

(1)![]() 的长度为________;
的长度为________;
操作证明:
(2)如图2,在(1)的条件下,将![]() 按如图放置,若
按如图放置,若![]() ,
,![]() 分别与
分别与![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() .请判断
.请判断![]() 和
和![]() 有怎样的数量关系,并证明结论;
有怎样的数量关系,并证明结论;

探究发现:
(3)如图3,在(1)的条件下,将![]() 按如图放置,若点
按如图放置,若点![]() 恰好在
恰好在![]() 上,求证:
上,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
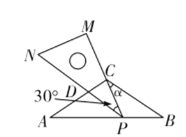
【题目】在综合实践课上,老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展数学活动.
已知,在等腰三角形纸片ABC中,CA=CB=5,∠ACB=120°,将一块含30°角的足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图所示放置,顶点P在线段BA上滑动(点P不与A,B重合),三角尺的直角边PM始终经过点C,并与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)特例感知
当∠BPC=110°时,α= °,点P从B向A运动时,∠ADP逐渐变 (填“大”或“小”).
(2)合作交流
当AP等于多少时,△APD≌△BCP,请说明理由.
(3)思维拓展
在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com