
【题目】在综合实践课上,老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展数学活动.
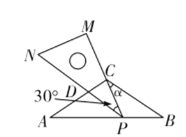
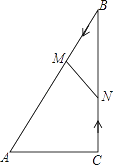
已知,在等腰三角形纸片ABC中,CA=CB=5,∠ACB=120°,将一块含30°角的足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图所示放置,顶点P在线段BA上滑动(点P不与A,B重合),三角尺的直角边PM始终经过点C,并与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)特例感知
当∠BPC=110°时,α= °,点P从B向A运动时,∠ADP逐渐变 (填“大”或“小”).
(2)合作交流
当AP等于多少时,△APD≌△BCP,请说明理由.
(3)思维拓展
在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.
【答案】(1)40°,小;(2)当AP=5时,△APD≌△BCP,理由详见解析;(3)当α=45°或90°时,△PCD是等腰三角形.
【解析】
(1)先根据三角形内角和定理求出∠B的度数,再一次运用三角形内角和定理即可求出![]() 的度数;根据三角形内角和定理即可判断点P从B向A运动时,∠ADP的变化情况;
的度数;根据三角形内角和定理即可判断点P从B向A运动时,∠ADP的变化情况;
(2)先根据三角形外角等于与它不相邻的两个内角和得到∠APC=∠B+α=30°+∠PCB,再证明∠APD=∠BCP,根据全等三角形的判定定理,即可得到当AP=5时,△APD≌△BCP.
(3)根据等腰三角形的判定,分三种情况讨论即可得到;
解:(1)∵CA=CB=5,∠ACB=120°,
∴∠B=∠A=![]() =30°,
=30°,
∴![]() ,
,
∵三角尺的直角边PM始终经过点C,
∴再移动的过程中,∠APN不断变大,∠A的度数没有变化,
∴根据三角形的内角和定理,得到∠ADP逐渐变小;
故答案为:40°,小.
(2)当AP=5时,△APD≌△BCP.
理由如下:∵∠ACB=120°,CA=CB,
∴∠A=∠B=30°.
又∵∠APC是△BPC的一个外角,
∴∠APC=∠B+α=30°+∠PCB,
∵∠APC=∠DPC+∠APD=30°+∠APD,
∴∠APD=∠BCP,
当AP=BC=5时,
在△APD和△BCP中,
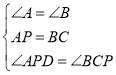
∴△APD≌△BCP(ASA);
(3)△PCD的形状可以是等腰三角形.
根据题意得:∠PCD=120°﹣α,∠CPD=30°,
有以下三种情况:
①当PC=PD时,△PCD是等腰三角形,
∴∠PCD=∠PDC=![]() =75°,即120°﹣α=75°,
=75°,即120°﹣α=75°,
∴α=45°;
②当DP=DC时,△PCD是等腰三角形,
∴∠PCD=∠CPD=30°,即120°﹣α=30°,
∴α=90°;
③当CP=CD时,△PCD是等腰三角形,
∴∠CDP=∠CPD=30°,
∴∠PCD=180°﹣2×30°=120°,
即120°﹣α=120°,
∴α=0°,
此时点P与点B重合,不符合题意,舍去.
综上所述,当α=45°或90°时,△PCD是等腰三角形.


科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点O是对角线BD中点,点E在边BC上,EO的延长线与边AD交于点F,连接BF、DE,如图1.

(1)求证:四边形BEDF是平行四边形;
(2)在(1)中,若DE=DC,∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、R,如图2.
①当CD=6,CE=4时,求BE的长.
②探究BH与AF的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,把4个长为a,宽为b的长方形拼成如图②所示的图形,且a=3b,则根据这个图形不能得到的等式是( )

A.(a+b)2=4ab+(a-b)2B.4b2+4ab=(a+b)2
C.(a-b)2=16b2-4abD.(a-b)2+12a2=(a+b)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+bx﹣1.
(1)求证:无论b取什么值,二次函数y=2x2+bx﹣1图象与x轴必有两个交点.
(2)若两点P(﹣3,m)和Q(1,m)在该函数图象上.
①求b、m的值;
②将二次函数图象向上平移多少单位长度后,得到的函数图象与x轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
阅读以下材料:
定义:两边分别相等且夹角互补的两个三角形叫做“互补三角形”.
用符号语言表示为:如图①,在△ABC与△DEF中,如果AC=DE,∠C+∠E=180°,BC=EF,那么△ABC与△DEF是互补三角形.
反之,“如果△ABC与△DEF是互补三角形,那么有AC=DE,∠C+∠E=180°,BC=EF”也是成立的.
自主探究
利用上面所学知识以及全等三角形的相关知识解决问题:
(1)性质:互补三角形的面积相等
如图②,已知△ABC与△DEF是互补三角形.
求证:△ABC与△DEF的面积相等.
证明:分别作△ABC与△DEF的边BC,EF上的高线,则∠AGC=∠DHE=90°.
…… (将剩余证明过程补充完整)
(2)互补三角形一定不全等,请你判断该说法是否正确,并说明理由,如果不正确,请举出一个反例,画出示意图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() (x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
(x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
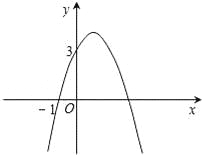
【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知长方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,由
上,由![]() 往
往![]() 运动,速度为
运动,速度为![]() ,运动时间为
,运动时间为![]() 秒,将
秒,将![]() 沿着
沿着![]() 翻折至
翻折至![]() ,点
,点![]() 对应点为
对应点为![]() ,
,![]() 所在直线与边
所在直线与边![]() 交与点
交与点![]() ,
,
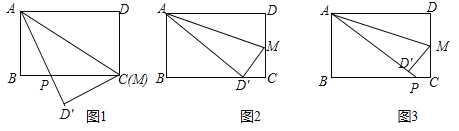
(1)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在边
恰好落在边![]() 上;
上;
(3)如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发, 在
出发, 在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,设运动时间为
匀速运动,设运动时间为![]() 秒
秒![]() ,连接
,连接![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 的面积为
的面积为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com