
����Ŀ���ۺ���ʵ��
�Ķ����²��ϣ�
���壺���߷ֱ�����Ҽнǻ��������������ν��������������Ρ���
�÷������Ա�ʾΪ����ͼ�٣��ڡ�ABC���DEF�У����AC=DE����C+��E=180�㣬BC=EF����ô��ABC���DEF�ǻ��������Σ�
��֮���������ABC���DEF�ǻ��������Σ���ô��AC=DE����C+��E=180�㣬BC=EF��Ҳ�dz����ģ�
����̽��
����������ѧ֪ʶ�Լ�ȫ�������ε����֪ʶ������⣺
��1�����ʣ����������ε�������
��ͼ�ڣ���֪��ABC���DEF�ǻ��������Σ�
��֤����ABC���DEF�������ȣ�
֤�����ֱ�����ABC���DEF�ı�BC��EF�ϵĸ��ߣ����AGC=��DHE=90����
���� (��ʣ��֤�����̲�������)
��2������������һ����ȫ�ȣ������жϸ�˵���Ƿ���ȷ����˵�����ɣ��������ȷ����ٳ�һ������������ʾ��ͼ��

���𰸡���1������������2������ȷ�����ɼ�����
��������
��1����֪��ABC����DEF�ǻ��������Σ��ɵá�ACB+��E=180����AC=DE��BC=EF��֤�á�ACG=��E��֤����AGC�ա�DHE���õ�AG=DH������![]() ������ABC����DEF�������ȣ�
������ABC����DEF�������ȣ�
��2������ȷ���Ȼ�������ͼ��֤����ABC�ա�DEF����ABC����DEF�ǻ��������Σ�����������һ����ȫ�ȵ�˵������
��1���ߡ�ABC����DEF�ǻ��������Σ�
���ACB+��E=180����AC=DE��BC=EF��
�֡ߡ�ACB+��ACG=180����
���ACG=��E��
����AGC����DHE��

���AGC�ա�DHE��AAS��
��AG=DH��
��![]()
����ABC����DEF�������ȣ�
��2������ȷ��
�������ͼ������ABC����DEF�У�

���ABC�ա�DEF��SAS����
���ABC����DEF�ǻ��������Σ�
���������һ����ȫ�ȵ�˵������



 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
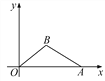
����Ŀ����ͼ����ֱ������ϵ�ڣ�OΪԭ�㣬��A������Ϊ(10��0)����B�ڵ�һ�����ڣ�BO��5��sin��BOA��![]() . ��(1)��B�����ꣻ(2)cos��BAO��ֵ��
. ��(1)��B�����ꣻ(2)cos��BAO��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵ�һ������������OC����x��ļн�Ϊ60�㣬������OC��ȡһ��A������A��AH��x ���ڵ�H����������y=x2��x��0����ȡһ��P����y����ȡһ��Q��ʹ����P��O��QΪ��������������AOHȫ�ȣ�����������ĵ�A��������______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ��������Σ�AB��AC���ֱ�������Ϊ�����ABC�����ȱ�������ADB�͵ȱ�������ACE�� ����DAE����DBC�����BAC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B������ֱ�Ϊ��1�� 4���ͣ�4�� 4����������![]() �Ķ������߶�AB���˶�����x�ύ��C��D���㣨C��D����ࣩ����C�ĺ�������СֵΪ-3�����D�ĺ��������ֵΪ_______��
�Ķ������߶�AB���˶�����x�ύ��C��D���㣨C��D����ࣩ����C�ĺ�������СֵΪ-3�����D�ĺ��������ֵΪ_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ۺ�ʵ�����ϣ���ʦ�ԡ���30������ǰ�͵���������ֽƬ��Ϊģ����ͬѧ�ǿ�չ��ѧ���
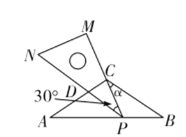
��֪���ڵ���������ֽƬABC�У�CA=CB=5����ACB=120�㣬��һ�麬30��ǵ��㹻���ֱ�����dz�PMN����M=90�㣬��MPN=30�㣩����ͼ��ʾ���ã�����P���߶�BA�ϻ�������P����A��B�غϣ������dzߵ�ֱ�DZ�PMʼ�վ�����C������CB�ļнǡ�PCB=����б��PN��AC�ڵ�D��
��1��������֪
����BPC��110��ʱ�������� ���㣬��P��B��A�˶�ʱ����ADP���� �������С������
��2����������
��AP���ڶ���ʱ����APD�ա�BCP����˵�����ɣ�
��3��˼ά��չ
�ڵ�P�Ļ��������У���PCD����״�����ǵ����������������ԣ�������нǦ��Ĵ�С���������ԣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������A��B��C�����ǿ����������������ƶ�����ش�
��1����A��B��C�ֱ��ʾ������______________________��
��2������B �����ƶ�������λ���Ⱥ��D����D��ʾ������_____________��
��3���ƶ���A�����E��ʹB��C��E�������������һ��Ϊ������������֮���߶ε��е㣬��ֱ��д�����е�A �ƶ��ľ���ͷ���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������OABC�ı�OA��y����������ϣ�OC��x����������ϣ�OA=AB=2��������y=![]() x2+bx+c������A��B������x���ڵ�D��E��OC�ϵĶ��㣨����C�غϣ�����EB����B����BF��BE��y����F
x2+bx+c������A��B������x���ڵ�D��E��OC�ϵĶ��㣨����C�غϣ�����EB����B����BF��BE��y����F
��1����b��c��ֵ��D������ꣻ
��2�����E��OC���˶�ʱ���ı���OEBF������������Ĺ����ԣ���֤����Ľ��ۣ�
��3������EF��BD����OE=m����BEF����BED�����֮��ΪS���ʣ���mΪ��ֵʱS��С������������Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ���abc��0 ��4a+2b+c��0 ��4ac��b2��8a ��![]() ��a��
��a��![]() ��b��c�����к�������ȷ���۵�ѡ���ǣ�������
��b��c�����к�������ȷ���۵�ѡ���ǣ�������

A. �٢� B. �٢ۢ� C. �ڢܢ� D. �٢ۢܢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com