
【题目】我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的腰长为2,“内角正度值”为45°,求该三角形的面积
【答案】1或2
【解析】试题分析:根据题意,分顶角为最小角和顶角为最大角两种情况求解即可.
试题解析:
当顶角为最大角时,设底角为x,则顶角为x+45°时,所以x+x+x+45°=180°,解得x=45°,所以此三角形为等腰直角三角形,此三角形的面积=![]() ×2×2=2;
×2×2=2;
当顶角为最小角时,设顶角为x时,则底角为x+45°,所以x+x+45°+x+45°=180°,解得x=30°,所以此三角形为顶点为30°的等腰三角形,AB=AC=2,∠A=30°,
作CD⊥AB于D,在Rt△ADC中,∵∠A=30°,
∴CD=![]() AC=1,
AC=1,
∴三角形ABC的面积=![]() CDAB=
CDAB=![]() ×1×2=1,
×1×2=1,
综上所述,该三角形的面积等于1或2.


科目:初中数学 来源: 题型:
【题目】已知函数y=![]() 的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )
的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学全体团员积极响应团委的号召,开展了“牵手儿童,奉献爱心”捐款活动.捐款活动结束后,某班班长将全班40名团员的捐款情况进行了统计,并绘制成如下的统计图.


(1)这40名团员捐款的中位数是________元,众数是________元;
(2)求这40名团员捐款的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:
如图1,已知点![]() 是正方形
是正方形![]() 的两条对角线的交点,以点
的两条对角线的交点,以点![]() 为直角顶点的直角三角形
为直角顶点的直角三角形![]() 的两边
的两边![]() ,
,![]() 分别过点
分别过点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.

(1)![]() 的长度为________;
的长度为________;
操作证明:
(2)如图2,在(1)的条件下,将![]() 按如图放置,若
按如图放置,若![]() ,
,![]() 分别与
分别与![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() .请判断
.请判断![]() 和
和![]() 有怎样的数量关系,并证明结论;
有怎样的数量关系,并证明结论;

探究发现:
(3)如图3,在(1)的条件下,将![]() 按如图放置,若点
按如图放置,若点![]() 恰好在
恰好在![]() 上,求证:
上,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)已知c=8![]() ,∠A=60°,求∠B,a,b;
,∠A=60°,求∠B,a,b;
(2)已知a=3![]() ,∠A=45°,求∠B,b,c.
,∠A=45°,求∠B,b,c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列是用火柴棒拼成的一组图形,第①个图形中有 3 根火柴棒,第②个图形中有 9 根火柴棒,第③个图形中有 18 根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是( ).
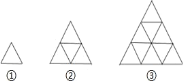
A. 63B. 60C. 56D. 45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com