
【题目】如图,拦水坝的横断面为等腰梯形ABCD,坝顶宽BC为6 m,坝高为3.2 m,为了提高水坝的拦水能力需要将水坝加高2 m,并且保持坝顶宽度不变,迎水坡CD的坡度不变,但是背水坡的坡度由原来的1∶2变成1∶2.5(坡度是坡高与坡的水平长度的比).求加高后的坝底HD的长为多少.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
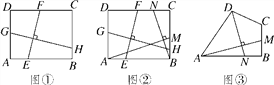
如图①,在矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() ;
;
【结论应用】
(2)如图②,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若![]() ,则
,则![]() 的值为 ;
的值为 ;
【联系拓展】
(3)如图③,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
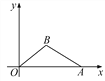
【题目】如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=![]() . 求:(1)点B的坐标;(2)cos∠BAO的值.
. 求:(1)点B的坐标;(2)cos∠BAO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:
如图1,已知点![]() 是正方形
是正方形![]() 的两条对角线的交点,以点
的两条对角线的交点,以点![]() 为直角顶点的直角三角形
为直角顶点的直角三角形![]() 的两边
的两边![]() ,
,![]() 分别过点
分别过点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.

(1)![]() 的长度为________;
的长度为________;
操作证明:
(2)如图2,在(1)的条件下,将![]() 按如图放置,若
按如图放置,若![]() ,
,![]() 分别与
分别与![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() .请判断
.请判断![]() 和
和![]() 有怎样的数量关系,并证明结论;
有怎样的数量关系,并证明结论;

探究发现:
(3)如图3,在(1)的条件下,将![]() 按如图放置,若点
按如图放置,若点![]() 恰好在
恰好在![]() 上,求证:
上,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
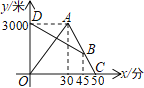
【题目】某天早晨,小童从家跑步去体育场锻炼,同时小郑从体育场晨练结束回家,途中两人相遇.小童跑到体育场后发现要下雨,立即按原路返回,遇到小郑后两人一起回到家(小童和小郑始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与小童出发的时间x(分)之间的函数图象.当x=_______时,小童与小郑相距600米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x 轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,分别以两腰为边向△ABC外作等边三角形ADB和等边三角形ACE. 若∠DAE=∠DBC,求∠BAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=![]() x2+bx+c经过点A,B,交正x轴于点D,E是OC上的动点(不与C重合)连接EB,过B点作BF⊥BE交y轴与F
x2+bx+c经过点A,B,交正x轴于点D,E是OC上的动点(不与C重合)连接EB,过B点作BF⊥BE交y轴与F
(1)求b,c的值及D点的坐标;
(2)求点E在OC上运动时,四边形OEBF的面积有怎样的规律性?并证明你的结论;
(3)连接EF,BD,设OE=m,△BEF与△BED的面积之差为S,问:当m为何值时S最小,并求出这个最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com