
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系![]() 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C 的相邻点,直线l为⊙C关于点P的相邻线.
(1)当⊙O的半径为1时,
①分别判断在点D(![]() ,
, ![]() ),E(0,﹣
),E(0,﹣![]() ),F(4,0)中,是⊙O的相邻点有 ;
),F(4,0)中,是⊙O的相邻点有 ;
②请从①中的答案中,任选一个相邻点,在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程;
③点P与点O的距离d满足范围___________________时,点P是⊙O的相邻点;
④点P在直线y=﹣x+3上,若点P为⊙O的相邻点,求点P横坐标x的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
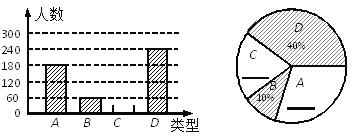
请根据以上信息回答:
(1) 将两幅不完整的图补充完整;
(2) 本次参加抽样调查的居民有多少人?
(3)若居民区有8000人,请估计爱吃D粽的人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、点F分别在边BC、DC上,BE=DF,∠EAF=60°.
(1)若AE=2,求EC的长;
(2)若点G在DC上,且∠AGC=120°,求证:AG=EG+FG.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com