
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C 的相邻点,直线l为⊙C关于点P的相邻线.
(1)当⊙O的半径为1时,
①分别判断在点D(![]() ,
, ![]() ),E(0,﹣
),E(0,﹣![]() ),F(4,0)中,是⊙O的相邻点有 ;
),F(4,0)中,是⊙O的相邻点有 ;
②请从①中的答案中,任选一个相邻点,在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程;
③点P与点O的距离d满足范围___________________时,点P是⊙O的相邻点;
④点P在直线y=﹣x+3上,若点P为⊙O的相邻点,求点P横坐标x的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.

【答案】(1)①D、E ② 证明见解析;③ 0≤d≤3且d≠1 ④0≤x≤3;(2) 0≤x≤9
【解析】试题分析:(1)由相邻点的定义可知:在圆C内的点必为相邻点,在圆C外的点必须满足,2AB2=PC2-1,其中A为PB的中点,且AB≤2,所以若半径为1的圆C有相邻点P,则PC的长必须满足0≤PC≤3且PC≠1,分别求出D、E、F到⊙O的距离即可判断.求出直线y=-x+3与坐标轴的交点坐标分别为(0,3)和(3,0),根据(1)问中结论可知,P的横坐标的取值范围是:0≤x≤3;
(2)根据(1)问中可知:0≤PC≤3且PC≠1,又因为点P在线段MN上移动,所以点C在以点P为圆心,半径为3的圆内,且不能在以点P为圆心,半径为1的圆上,再根据点C在x轴上,即可得出C的横坐标取值范围.
试题解析:(1)由定义可知,
当点P在⊙C内时,
由垂径定理可知,点P必为⊙C的相邻点,
此时,0≤PC<1;
当点P在⊙C外时,设点A是PB的中点,连接PC交⊙C于点M,延长PC交⊙C于点N,连接AM,BN,

∵∠AMP+∠NMA=180°,
∠B+∠NMA=180°,
∴∠AMP=∠B,
∵∠P=∠P,
∴△AMP∽△NBP,
∴![]() ,
,
∴PAPB=PMPN,
∵点A是PB的中点,
∴AB=PA,
又∵⊙C的半径为1,
∴2AB2=(PC-CM)(PC+CN),
∴2AB2=PC2-1,
又∵AB是⊙C的弦,
∴AB≤2,
∴2AB2≤8,
∴PC2-1≤8,
∴PC2≤9,
∴PC≤3,
∵点P在⊙C外,
∴PC>1,
∴1<PC≤3,
当点P在⊙C上时,
此时PC=1,但不符合题意,
综上所述,半径为1的⊙C,当点P与圆心C的距离满足:0≤PC≤3,且PC≠1时,点P为⊙C的相邻点;

①∵D(![]() ,
, ![]() ),
),
∴DO= ,
,
∵E(0,-![]() ),
),
∴OE=![]() ,
,
∵F(4,0),
∴OF=4,
∴D和E是⊙O的相邻点;
②连接OD,过点D作OD的垂线交⊙O于A、B两点;

③令x=0代入y=-x+3,
∴y=3,
令y=0代入y=-x+3,
∴x=3,
∴y=-x+3与坐标轴的交点为(0,3)和(3,0)
∵由于点P在直线y=-x+3上,且点P是⊙O的相邻点,
∴0≤PO≤3,且PO≠1
又∵点P在⊙O外,
∴1<PO≤3,
∴p的横坐标范围为:0≤x≤3;
(2)令x=0代入y=-![]() x+2
x+2![]() ,
,
∴y=2![]() ,
,
∴N(0,2![]() ),
),
令y=0代入y=-![]() x+2
x+2![]() ,
,
∴x=6,
∴M(6,0),
∵点P是半径为1的⊙C的相邻点,
∴0≤PC≤3且PC≠1,
∴点C在以点P为圆心,半径为3的圆内,且不能在以点P为圆心,半径为1的圆上,
∵点C在x轴上,
∴点C的横坐标范围的取值范围:0≤x≤9.



科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠C=90°,AB=5,BC=3,S、Q两点同时分别从A、C出发,点S以每秒2个单位的速度沿着AC向点C运动,点Q以每秒1个单位的速度沿着CB向点B运动.当其中一点到达终点时,另一点也随之停止运动
(1)求几秒时SQ的长为2
(2)求几秒时,△SQC的面积最大,最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系![]() 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
查看答案和解析>>
科目:初中数学 来源: 题型:
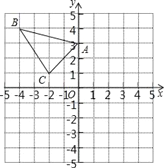
【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别把带有指针的圆形转盘A、B分成4等份、3等份的扇形区域,并在每一个小区域内标上数字(如图所示).欢欢、乐乐两个人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为奇数,则欢欢胜;若指针所指两区域的数字之积为偶数,则乐乐胜;若有指针落在分割线上,则无效,需重新转动转盘.
(1)试用列表或画树状图的方法,求欢欢获胜的概率;
(2)请问这个游戏规则对欢欢、乐乐双方公平吗?试说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com