Question

【题目】如图，在正方形ABCD中，点E、点F分别在边BC、DC上，BE=DF，∠EAF=60°．

（1）若AE=2，求EC的长；

（2）若点G在DC上，且∠AGC=120°，求证：AG=EG+FG．

Answer 1

【答案】（1）（2）证明见解析

【解析】试题分析：（1）连接EF，根据正方形的性质求出AB=AD，∠B=∠D，然后利用“边角边”证明△ABE和△ADF全等，根据全等三角形对应边相等可得AE=AF，从而得到△AEF是等边三角形，根据等边三角形的三条边都相等可得EF，再判断出△CEF是等腰直角三角形，根据等腰直角三角形的直角边与斜边的关系求解即可；

（2）在AG上截取GH=FG，可得△FGH是等边三角形，根据等边三角形的性质可得FH=FG，∠FHG=60°，再求出∠AFH=∠EFG，然后利用“边角边”证明△AFH和△EFG全等，根据全等三角形对应边相等AH=GE，然后证明即可．

试题解析：（1）解：如图，连接EF，

在正方形ABCD中，AB=AD，∠B=∠D，

在△ABE和△ADF中， ，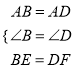

∴△ABE≌△ADF（SAS），

∴AE=AF，

∵∠EAF=60°，

∴△AEF是等边三角形，

∴EF=AE=2，

∵BE=DF，BC=CD，

∴BC﹣BE=CD﹣DF，

即CE=CF，

∴△CEF是等腰直角三角形，

∴EC=EF=×2=；

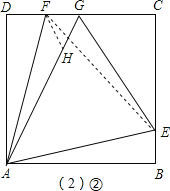
（2）如图（2）②在AG上截取GH=FG，

∵∠AGC=120°，

∴∠AGF=60°，

∴△FGH是等边三角形，

∴FH=FG，∠FHG=60°，

∵△AEF是等边三角形，

∴∠AFE=60°，

∴∠AFE=∠GFH=60°，

∴∠AFE﹣∠EFH=∠GFH﹣∠EFH，

即∠AFH=∠EFG，

在△AFH和△BFG中， ，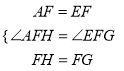

∴△AFH≌△EFG（SAS），

∴AH=GE，

∴AG=AH+GH=EG+FG，

即AG=EG+FG．