
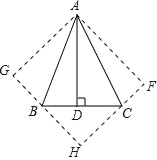
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
(1)求证:四边形AFHG为正方形;
(2)若BD=6,CD=4,求AB的长.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)由折叠的性质可得到的条件是:①AG=AD=AF,②∠GAF=∠GAD+∠DAF=2∠BAC=90°,且∠G=∠F=90°;由②可判定四边形AGHF是矩形,由AG=AF可证得四边形AGHF是正方形;
(2)设AD=x,由折叠的性质可得:AD=AF=x(即正方形的边长为x),BG=BD=6,CF=CD=4;进而可用x表示出BH、HC的长,即可在Rt△BHC中,由勾股定理求得AD的长,进而可求出AB的长.
试题解析:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°;
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,
∠BAG=∠BAD,∠CAF=∠CAD,
∴∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°;
∴∠GAF=∠BAG+∠CAF+∠BAC=90°;
∴四边形AFHG是正方形;
(2)∵四边形AFHG是正方形,
∴∠BHC=90°,
又GH=HF=AD,GB=BD=6,CF=CD=4,
设AD的长为x,则BH=GH﹣GB=x﹣6,CH=HF﹣CF=x﹣4,
在Rt△BCH中,BH2+CH2=BC2,
∴(x﹣6)2+(x﹣4)2=102,
解得x1=12,x2=﹣2(不合题意,舍去),
∴AD=12,
∴AB=![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】贵成高铁开通后极大地方便了人们的出行,甲、乙两个城市相距450千米,加开高铁列车后,高铁列车行驶时间比原特快列车行驶时间缩短了3小时,已知高铁列车平均行驶速度是原特快列车平均行驶速度的3倍,求高铁列车的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )
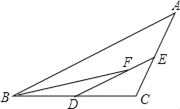
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明化简分式的过程,仔细阅读并解答所提出的问题
解:![]()
![]() 第一步
第一步
=2(x2)(x6)第二步
=2x4x6第三步
![]() 第四步
第四步
(1)小明的解法从第 步开始出现错误;
(2)第一步进行 ,它的数学依据是 .
(3)第三步进行 ,它的数学依据是 .
(4)正确的化简结果是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=﹣x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)档这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
【答案】(1)取值范围为1100元/人~1200元/人之间;(2)50000;(3)x=900时,w最大=160000
【解析】试题分析:(1)根据题意列不等式求解可;
(2)根据报价减去成本可得到函数的解析式,根据一次函数的图像求解即可;
(3)根据利润等于人次乘以价格即可得到函数的解析式,然后根据二次函数的最值求解即可.
试题解析:(1)∵由题意得![]() 时,即
时,即![]() ,
,
∴解得![]()
即要将该旅游线路每月游客人数控制在200人以内,该旅游线路报价的取值范围为1100元/人~1200元/人之间;
(2)![]() ,
,![]() ,∴
,∴![]()
∵![]() ,∴当
,∴当![]() 时,z最低,即
时,z最低,即![]() ;
;
(3)利润![]()
当![]() 时,
时,![]() .
.
【题型】解答题
【结束】
23
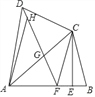
【题目】已知四边形ABCD中,AB=AD,对角线AC平分∠DAB,过点C作CE⊥AB于点E,点F为AB上一点,且EF=EB,连接DF.
(1)求证:CD=CF;
(2)连接DF,交AC于点G,求证:△DGC∽△ADC;
(3)若点H为线段DG上一点,连接AH,若∠ADC=2∠HAG,AD=3,DC=2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
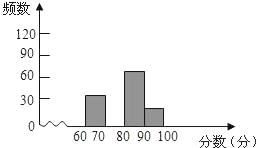
【题目】为迎接国庆60周年,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x<100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)表中m和n所表示的数分别为:m= ,n= ;
(2)请在图中,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段;
(4)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com