
【题目】在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )
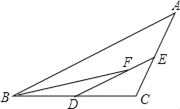
A. 1B. 2C. 3D. 4
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
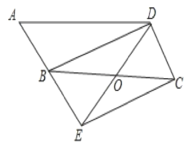
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD=___°时,四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知张强家、体育场、文具店在同一直线上,下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中![]() 表示时间,
表示时间,![]() 表示张强离家的距离.
表示张强离家的距离.

根据图象解答下列问题:
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
(2)体育场离文具店多远?
(3)张强在文具店停留了多少时间?
(4)求张强从文具店回家过程中![]() 与
与![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元。
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购进这两种型号的节能灯共80只,并且A型节能灯的数量不多于B型节能灯的3倍,问如何购买最省钱,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种商品,若购进A种商品20件和B种商品15件需380元;若购进A种商品15件和B种商品10件需280元.
(1)求A、B两种商品的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过900元,问最多能购进A种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
(1)求证:四边形AFHG为正方形;
(2)若BD=6,CD=4,求AB的长.
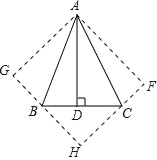
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表,从左边第1个格子开始依次在每个格子中填入一个正整数,第1个格子填入![]() ,第2个格子填入
,第2个格子填入![]() ,第3个格子填入
,第3个格子填入![]() ,…,第n个格子填入
,…,第n个格子填入![]() ,以此类推. 表中任意4个相邻格子中所填正整数之和都相等,其中
,以此类推. 表中任意4个相邻格子中所填正整数之和都相等,其中![]() .
.
|
|
|
| … |
| … |
(1)若![]() ,求
,求![]() ;
;![]() ;
;
(2)将表中前2020个数的和记为S,若![]() ,求S的值.
,求S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com