练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】学校准备购进一批节能灯，已知1只A型节能灯和3只B型节能灯共需26元；3只A型节能灯和2只B型节能灯共需29元。

    （1）求1只A型节能灯和1只B型节能灯的售价各是多少元？

    （2）学校准备购进这两种型号的节能灯共80只，并且A型节能灯的数量不多于B型节能灯的3倍，问如何购买最省钱，说明理由。

    【答案】（1）1只A型节能灯的售价为5元，1只B型节能灯的售价为7元；（2）购买60只A型节能灯，20只B型节能灯最省钱,理由见解析

    【解析】

    （1）设一只A型节能灯的售价是x元，一只B型节能灯的售价y元，根据题意列出方程组，求出方程组的解即可；

    （2）设A型节能灯买了a只，则B型节能灯买了（80-a）只，共花费w元，根据题意列出不等式组，求出不等式组的解集即可.

    解（1）设1只A型节能灯的售价为x元，1只B型节能灯的售价为y元

    由题意得：

    解得：

    答：1只A型节能灯的售价为5元，1只B型节能灯的售价为7元

    （2）设购买A型节能灯a个，则购买B型节能灯（80-a）个，总费用为w元

    由题意得：a≤3（80-a）

    解得a≤60

    又∵w=5a+7（80-a）=-2a+560

    ∴w随a的增大而减小

    ∴当a取最大值60时，w有最小值

    w=-2×60+560=440

    即购买60只A型节能灯，20只B型节能灯最省钱

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

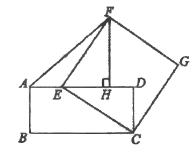
    【题目】如图，在矩形ABCD中，AD=4，点E在边AD上，连接CE，以CE为边向右上方作正方形CEFG，作FH⊥AD，垂足为H，连接AF．

    (1)求证：FH=ED；

    (2)当AE为何值时，△AEF的面积最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

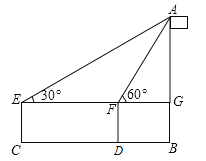
    【题目】如图，小丽准备测一根旗杆AB的高度，已知小丽的眼睛离地面的距离EC=1.5米，第一次测量点C和第二次测量点D之间的距离CD=10米，∠AEG=30°，∠AFG=60°，请你帮小丽计算出这根旗杆的高度．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】贵成高铁开通后极大地方便了人们的出行，甲、乙两个城市相距450千米，加开高铁列车后，高铁列车行驶时间比原特快列车行驶时间缩短了3小时，已知高铁列车平均行驶速度是原特快列车平均行驶速度的3倍，求高铁列车的平均行驶速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（探索新知）

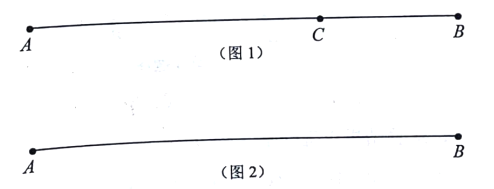
    如图1，点在线段上，图中共有3条线段：、和，若其中有一条线段的长度是另一条线段长度的两倍，则称点是线段的“二倍点”.

    （1）①一条线段的中点 这条线段的“二倍点”；（填“是”或“不是”）

    ②若线段，是线段的“二倍点”，则 （写出所有结果）

    （深入研究）

    如图2，若线段，点从点的位置开始，以每秒2的速度向点运动，当点到达点时停止运动，运动的时间为秒.

    （2）问为何值时，点是线段的“二倍点”；

    （3）同时点从点的位置开始，以每秒1的速度向点运动，并与点同时停止.请直接写出点是线段的“二倍点”时的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，D、E分别是BC、AC中点，BF平分∠ABC．交DE于点F．AB＝8，BC＝6，则EF的长为(　　)

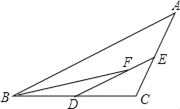
    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（1）13+（－18）－（6－11）

    （2）÷

    （3）－14－×[2－(－3)2]

    （4）a－2b－[－4a＋(c＋3b)]

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某旅行社推出一条成本价位500元/人的省内旅游线路，游客人数y（人/月）与旅游报价x（元/人）之间的关系为y=﹣x+1300，已知：旅游主管部门规定该旅游线路报价在800元/人～1200元/人之间．

    （1）要将该旅游线路每月游客人数控制在200人以内，求该旅游线路报价的取值范围；

    （2）求经营这条旅游线路每月所需要的最低成本；

    （3）档这条旅游线路的旅游报价为多少时，可获得最大利润？最大利润是多少？

    【答案】（1）取值范围为1100元/人～1200元/人之间；（2）50000；（3）x=900时，w最大=160000

    【解析】试题分析：（1）根据题意列不等式求解可；

    （2）根据报价减去成本可得到函数的解析式，根据一次函数的图像求解即可；

    （3）根据利润等于人次乘以价格即可得到函数的解析式，然后根据二次函数的最值求解即可.

    试题解析：（1）∵由题意得时，即，

    ∴解得

    即要将该旅游线路每月游客人数控制在200人以内，该旅游线路报价的取值范围为1100元/人~1200元/人之间；

    （2），，∴

    ∵，∴当时，z最低，即；

    （3）利润

    当时，.

    【题型】解答题
    【结束】
    23

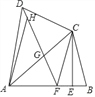
    【题目】已知四边形ABCD中，AB=AD，对角线AC平分∠DAB，过点C作CE⊥AB于点E，点F为AB上一点，且EF=EB，连接DF．

    （1）求证：CD=CF；

    （2）连接DF，交AC于点G，求证：△DGC∽△ADC；

    （3）若点H为线段DG上一点，连接AH，若∠ADC=2∠HAG，AD=3，DC=2，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

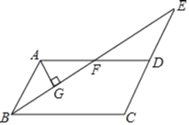
    【题目】如图，在平行四边形ABCD中，∠ABC的平分线与CD的延长线交于点E，与AD交于点F，且点F恰好为边AD的中点．

    （1）求证：△ABF≌△DEF；

    （2）若AG⊥BE于G，BC＝4，AG＝1，求BE的长．

    查看答案和解析>>

    同步练习册答案