
����Ŀ����̽����֪��
��ͼ1����![]() ���߶�
���߶�![]() �ϣ�ͼ�й���3���߶Σ�
�ϣ�ͼ�й���3���߶Σ�![]() ��
��![]() ��
��![]() ����������һ���߶εij�������һ���߶γ��ȵ���������Ƶ�
����������һ���߶εij�������һ���߶γ��ȵ���������Ƶ�![]() ���߶�
���߶�![]() �ġ������㡱.
�ġ������㡱.
��1����һ���߶ε��е� �����߶εġ������㡱������ǡ����ǡ���
�����߶�![]() ��
��![]() ���߶�
���߶�![]() �ġ������㡱����
�ġ������㡱����![]() ��д�����н����
���������
���������
��ͼ2�����߶�![]() ����
����![]() �ӵ�
�ӵ�![]() ��λ�ÿ�ʼ����ÿ��2
��λ�ÿ�ʼ����ÿ��2![]() ���ٶ����
���ٶ����![]() �˶�������
�˶�������![]() �����
�����![]() ʱֹͣ�˶����˶���ʱ��Ϊ
ʱֹͣ�˶����˶���ʱ��Ϊ![]() ��.
��.
��2����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ���߶�
���߶�![]() �ġ������㡱��
�ġ������㡱��
��3��ͬʱ��![]() �ӵ�
�ӵ�![]() ��λ�ÿ�ʼ����ÿ��1
��λ�ÿ�ʼ����ÿ��1![]() ���ٶ����
���ٶ����![]() �˶��������
�˶��������![]() ͬʱֹͣ.��ֱ��д����
ͬʱֹͣ.��ֱ��д����![]() ���߶�
���߶�![]() �ġ������㡱ʱ
�ġ������㡱ʱ![]() ��ֵ.
��ֵ.
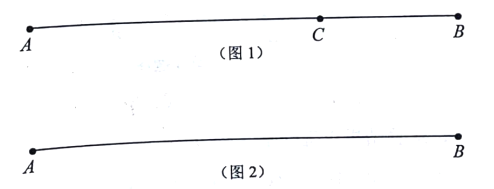
���𰸡���1�����ǣ���10��![]() ��
��![]() ����2��5��
����2��5��![]() ��
��![]() ����3��8��
����3��8��![]() ��
��![]()
��������
��1���ٿ�ֱ�Ӹ��ݡ������㡱�Ķ�������жϣ�
�ڿɷ�Ϊ��������������ۣ��ֱ����BC�ij��ȼ��ɣ�
��2���ú�t�Ĵ���ʽ�ֱ��ʾ���߶�AM��BM��AB��Ȼ����ݡ������㡱�����壬�������۵ý����
��3���ú�t�Ĵ���ʽ�ֱ��ʾ���߶�AN��NM��AM��Ȼ����ݡ������㡱�����壬�������ۣ�
�⣺��1������Ϊ�߶ε��е�Ѹ��߶ηֳ���ȵ������֣�
���߶ε���2�����е�һ����߶γ���
��һ���߶ε��е��������߶εġ������㡱
�ʴ�Ϊ����.
�ڡ�![]() ��
��![]() ���߶�
���߶�![]() ��������������
��������������
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
�ʴ�Ϊ��10��![]() ��
��![]() ��
��
��2����AM=2BMʱ��20-2t=2��2t����ã�t=![]() ��
��
��AB=2AMʱ��20=2����20-2t������ã�t=5��
��BM=2AMʱ��2t=2����20-2t������ã�t=![]() ��
��
��tΪ![]() ��5��
��5��![]() ʱ����M���߶�AB�ġ������㡱��
ʱ����M���߶�AB�ġ������㡱��
��3����AN=2MNʱ��t=2[t-��20-2t��]����ã�t=8��
��AM=2NMʱ��20-2t=2[t-��20-2t��]����ã�t=![]() ��
��
��MN=2AMʱ��t-��20-2t��=2��20-2t������ã�t=![]() ��
��
��tΪ![]() ��8��
��8��![]() ʱ����M���߶�AN�ġ������㡱��
ʱ����M���߶�AN�ġ������㡱��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
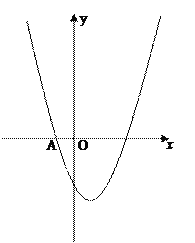
����Ŀ����֪������y=x2+bx��3��b�dz�����������A����1��0����
��1����������ߵĽ���ʽ�Ͷ������ꣻ
��2��P��m��t��Ϊ�������ϵ�һ�����㣬P����ԭ��ĶԳƵ�ΪP'��
�� ����P' ���ڸ���������ʱ����m��ֵ��
�� ����P' ���ڵڶ������ڣ�P'A2ȡ����Сֵʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����������ϵ�ԭ�㿪ʼ���������ƶ�3����λ���ȣ��������ƶ�5����λ���ȣ����Կ����յ��ʾ������![]() ��
��

��֪��A�������ϵĵ㣬������и��⣺
��1�������A��ʾ������3������A�������ƶ�7����λ���ȣ��������ƶ�5����λ���ȣ���ô�յ�B��ʾ������__________��A��B�����ľ���Ϊ__________��
��2�������A��ʾ�����ǣ�4������A�������ƶ�168����λ���ȣ��������ƶ�256����λ���ȣ���ô�յ�B��ʾ������__________��A��B�����ľ���Ϊ__________��
��3��һ��أ������A��ʾ������m������A�������ƶ�n����λ���ȣ��������ƶ�t����λ���ȣ���ô�յ�B��ʾ������__________��A��B�����ľ���Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a�����ĸ�������b��-5���෴����c=-|-2|����a��b��c�ֱ��ǵ�A��B��C�������϶�Ӧ������
![]()
��1����a��b��c��ֵ�����������ϱ����A��B��C��
��2��������P�ӵ�A�����������������˶�������Qͬʱ�ӵ�B����Ҳ�������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��1����λ���ȣ����˶������P�����ϵ�Q��
��3������������һ��M��ʹ��M��A��B��C����ľ���֮�͵���12����������е�M��Ӧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB����COD�ǵ���ֱ�������Σ���D��AB�ϣ�
��1����֤����AOC�ա�BOD��
��2����AD=3��BD=1����CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������һ�����ܵƣ���֪1ֻA�ͽ��ܵƺ�3ֻB�ͽ��ܵƹ���26Ԫ��3ֻA�ͽ��ܵƺ�2ֻB�ͽ��ܵƹ���29Ԫ��
��1����1ֻA�ͽ��ܵƺ�1ֻB�ͽ��ܵƵ��ۼ۸��Ƕ���Ԫ��
��2��ѧУ�������������ͺŵĽ��ܵƹ�80ֻ������A�ͽ��ܵƵ�����������B�ͽ��ܵƵ�3��������ι�����ʡǮ��˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ҹ���ѧ������Ѹ�ͷ�չ���ܶ���ҵ�Ѿ��ɡ��й����족����Ϊ���й����족��������ҵ�ǡ��й����족�ĵ䷶���ס����������еĻ�վ���1280ǧ�ף��ӿ������Ӽ�վ����վ������ʱ��������11��Сʱ����������dz��У���֪������ʻ�ٶ���ԭ�����ٶȵ�3.2�������������ʻ�ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
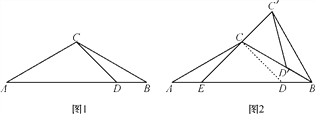
����Ŀ����ͼ1����ABC�У�AC��BC����A��30�㣬��D��AB���ϣ��ҡ�ADC��45��.
(1)���BCD�Ķ�����
(2)��ͼ1�еġ�BCD�Ƶ�B˳ʱ����ת�õ���BC��D�䣬����D��ǡ������BC����ʱ����ͼ2��ʾ������C��C���ӳ���AB�ڵ�E.
�����C��CB�Ķ�����
����֤����C��BD��ա�CAE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
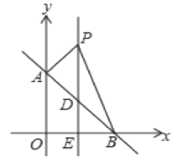
����Ŀ����ͼ,ƽ��ֱ������ϵ��,ֱ��AB:y=x+b��y���ڵ�A(0,4)����x���ڵ�B.
(1)���B�����ꣻ
(2)ֱ��l��ֱƽ��OB��AB�ڵ�D����x���ڵ�E����P��ֱ��l��һ���㣬���ڵ�D���Ϸ������P��������Ϊn.
���ú�n�Ĵ���ʽ��ʾ��ABP�������
�ڵ�S��ABP=8ʱ�����P�����ꣻ
(3)��(2)�Тڵ������£���PBΪб��������ֱ�ǡ�PBC�����C�����ꡣ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com