练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】近年来，随着我国科学技术的迅猛发展，很多行业已经由“中国制造”升级为“中国创造”，高铁事业是“中国创造”的典范，甲、乙两个城市的火车站相距1280千米，加开高铁后，从甲站到乙站的运行时间缩短了11个小时，大大方便了人们出行，已知高铁行驶速度是原来火车速度的3.2倍，求高铁的行驶速度．

    【答案】高铁的行驶速度为256千米/时．

    【解析】

    设原来火车的速度为x千米/时，则高铁的速度为3.2x千米/时，根据时间=路程÷速度结合高铁比原来的火车省11小时，即可得出关于x的分式方程，解之即可得出结论．

    设原来火车的速度为x千米/时，则高铁的速度为3.2x千米/时，

    根据题意得：，

    解得：x＝80，

    经检验，x＝80是原分式方程的解，

    ∴3.2x＝3.2×80＝256．

    答：高铁的行驶速度为256千米/时．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

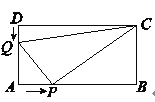
    【题目】如图所示，在矩形中，，点沿边从点开始向点以的速度移动，点沿边从点开始向点以的速度移动，如果点同时出发，用表示移动的时间（）．

    （1）当为何值时，为等腰三角形？

    （2）求四边形的面积，并探索一个与计算结果有关的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

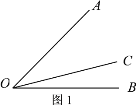
    【题目】如图 1，射线 OC在∠AOB的内部，图中共有 3个角：∠AOB、∠AOC 和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线 OC是∠AOB的奇妙线．

    （1）一个角的角平分线_______这个角的奇妙线．（填是或不是）；

    （2）如图 2，若∠MPN＝60°，射线 PQ绕点 P从 PN位置开始，以每秒 10°的速度逆时针旋转，当∠QPN首次等于 180°时停止旋转，设旋转的时间为 t（s）．

    ① 当 t为何值时，射线 PM是∠QPN 的奇妙线？

    ②若射线 PM 同时绕点 P以每秒 5°的速度逆时针旋转，并与 PQ同时停止旋转．请求出当射线 PQ是∠MPN的奇妙线时 t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（探索新知）

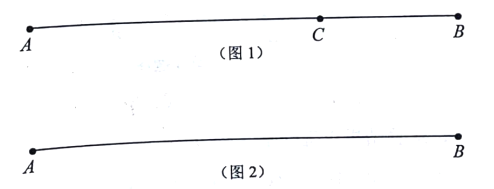
    如图1，点在线段上，图中共有3条线段：、和，若其中有一条线段的长度是另一条线段长度的两倍，则称点是线段的“二倍点”.

    （1）①一条线段的中点 这条线段的“二倍点”；（填“是”或“不是”）

    ②若线段，是线段的“二倍点”，则 （写出所有结果）

    （深入研究）

    如图2，若线段，点从点的位置开始，以每秒2的速度向点运动，当点到达点时停止运动，运动的时间为秒.

    （2）问为何值时，点是线段的“二倍点”；

    （3）同时点从点的位置开始，以每秒1的速度向点运动，并与点同时停止.请直接写出点是线段的“二倍点”时的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（ ）.

    A. OA＝OC，OB＝OD B. ∠BAD＝∠BCD，AB∥CD

    C. AD∥BC，AD＝BC D. AB＝CD，AO＝CO

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（1）13+（－18）－（6－11）

    （2）÷

    （3）－14－×[2－(－3)2]

    （4）a－2b－[－4a＋(c＋3b)]

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M，N分别是斜边AB，DE的中点，点P为AD的中点，连接AE、BD、MN．

    (1)求证：△PMN为等腰直角三角形；

    (2)现将图①中的△CDE绕着点C顺时针旋转α(0°＜α＜90°)，得到图②，AE与MP，BD分别交于点G、H，请判断①中的结论是否成立，若成立，请证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=50°，则∠DA′E′的大小为（ ）

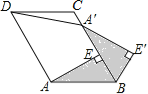
    A. 130° B. 150° C. 160° D. 170°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤．通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤．为了保证每天至少售出260斤，张阿姨决定降价销售．

    （1）若将这种水果每斤的售价降低x元，则每天的销售量是 斤（用含x的代数式表示）；

    （2）销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？

    （3）当每斤的售价定为多少元时，每天获利最大？最大值为多少？

    查看答案和解析>>

    同步练习册答案