
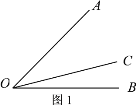
【题目】如图 1,射线 OC在∠AOB的内部,图中共有 3个角:∠AOB、∠AOC 和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线 OC是∠AOB的奇妙线.
(1)一个角的角平分线_______这个角的奇妙线.(填是或不是);
(2)如图 2,若∠MPN=60°,射线 PQ绕点 P从 PN位置开始,以每秒 10°的速度逆时针旋转,当∠QPN首次等于 180°时停止旋转,设旋转的时间为 t(s).
① 当 t为何值时,射线 PM是∠QPN 的奇妙线?
②若射线 PM 同时绕点 P以每秒 5°的速度逆时针旋转,并与 PQ同时停止旋转.请求出当射线 PQ是∠MPN的奇妙线时 t的值.


【答案】(1)是;(2) ①当t的值是9或12或18时,射线 PM是∠QPN 的奇妙线;②当射线 PQ是∠MPN的奇妙线时 t的值为![]() 或4或6.
或4或6.
【解析】
(1)根据奇妙线定义即可求解;
(2)①分3种情况,根据奇妙线定义列方程求解即可;
②分3种情况,根据奇妙线定义列方程求解即可.
解:(1) 一个角的平分线是这个角的“奇妙线”;
(2) ①∠MPN=60,∠QPM=10t-60,∠QPN=10t(最大角),
当∠MPN=2∠QPM时,60=2(10t-60),解得t=9;
当∠QPN=2∠MPN时,10t =2×60,解得t=12;
当∠QPM=2∠MPN时,10t-60=2×60,解得t=18;
综上,当t的值是9或12或18时,射线 PM是∠QPN 的奇妙线.
②∠QPN=10t,∠QPM=60-10t+5t=60-5t,∠MPN=60+5t(最大角),
当∠QPM=2∠QPN时, 60-5t =2×10t ,解得t=![]() ;
;
当∠MPN=2∠QPN时,60+5t =2×10t,解得t=4;
当∠QPN=2∠QPM时,10t =2×(60-5t),解得t=6;
综上,当射线 PQ是∠MPN的奇妙线时 t的值为![]() 或4或6.
或4或6.
故答案为:(1)是;(2) ①当t的值是9或12或18时,射线 PM是∠QPN 的奇妙线;②当射线 PQ是∠MPN的奇妙线时 t的值为![]() 或4或6.
或4或6.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】一个长方体纸盒的平面展开图如图所示,纸盒中相对两个面上的数互为相反数.
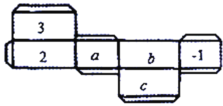
(1)填空:![]() ________,
________,![]() ________,
________,![]() ________.
________.
(2)先化简,再求值:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乔亚萍做一道数学题,“已知两个多项式![]()
![]() ,
,![]() ,试求
,试求![]() .”其中多项式
.”其中多项式![]() 的二次项系数印刷不清楚
的二次项系数印刷不清楚
(1)乔亚萍看了答案以后知道![]() ,请你替乔亚萍求出多项式
,请你替乔亚萍求出多项式![]() 的二次项系数;
的二次项系数;
(2)在(1)的基础上,乔亚萍已经将多项式![]() 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式![]() ,要求乔亚萍求出
,要求乔亚萍求出![]() 的结果.乔亚萍在求解时,误把“
的结果.乔亚萍在求解时,误把“![]() ”看成“
”看成“![]() ”,结果求出的答案为
”,结果求出的答案为![]() ,请你替乔亚萍求出“
,请你替乔亚萍求出“![]() ”的正确答案.
”的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是![]() 。
。

已知点A是数轴上的点,完成下列各题:
(1)如果点A表示的数是3,将点A先向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________;
(2)如果点A表示的数是-4,将点A先向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________;
(3)一般地,如果点A表示的数是m,将点A先向右移动n个单位长度,再向左移动t个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
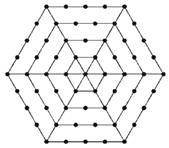
(1)填写下表:
层数 | 1 | 2 | 3 | 4 | 5 | 6 |
该层对应的点数 | 1 | 6 | _____ | 18 | _____ | _____ |
(2)写出第n层所对应的点数为_____;
(3)如果某一层共96个点,那么它是第_____层,此时所有层中共有_____个点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b是-5的相反数,c=-|-2|,且a、b、c分别是点A、B、C在数轴上对应的数.
![]()
(1)求a、b、c的值,并在数轴上标出点A、B、C.
(2)若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点P可以追上点Q?
(3)在数轴上找一点M,使点M到A、B、C三点的距离之和等于12,请求出所有点M对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,随着我国科学技术的迅猛发展,很多行业已经由“中国制造”升级为“中国创造”,高铁事业是“中国创造”的典范,甲、乙两个城市的火车站相距1280千米,加开高铁后,从甲站到乙站的运行时间缩短了11个小时,大大方便了人们出行,已知高铁行驶速度是原来火车速度的3.2倍,求高铁的行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,鼓楼区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中某些家庭一年的月平均用水量(单位:吨),调查中发现,每户用水量每月均在10﹣14吨范围,并将调查结果制成了如图所示的条形统计图(不完整)和扇形统计图.
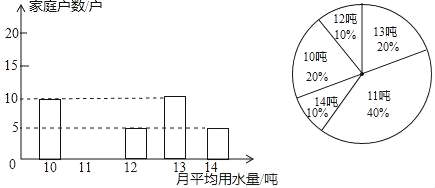
(1)请将条形统计图补充完整;
(2)这些家庭月用水量数据的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计鼓楼区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com