
����Ŀ��Ϊ�˳�������Լ��ˮ���������𡱣���¥��������������ֱ������300����ͥ����ˮ�����һ�ε��飬����������С��������������ijЩ��ͥһ�����ƽ����ˮ������λ���֣��������з��֣�ÿ����ˮ��ÿ�¾���10��14�ַ�Χ�������������Ƴ�����ͼ��ʾ������ͳ��ͼ����������������ͳ��ͼ��
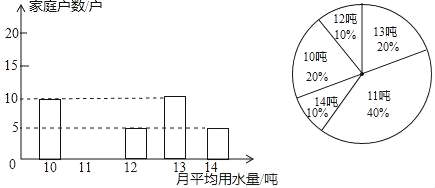
��1���뽫����ͳ��ͼ����������
��2����Щ��ͥ����ˮ�����ݵ�ƽ�������� ������������ ������λ������ ����
��3�������������ݣ����ƹ�¥��ֱ������300����ͥ����ƽ����ˮ��������12�ֵ�Լ�ж��ٻ���
���𰸡���1�������������2��11.6��11��11����3��210(��).
��������
(1)�ȸ���ͳ��ͼ�е������������������Ȼ������õ�������������11�ֵ��û�ռ�İٷֱȼ��ɵó���,�ٲ�ȫ����;
(2)��������,��λ���Լ�ƽ�����Ĺ�ʽ���м��㼴��;
(3)���������в�����12�ֵĻ���,�ٹ���300����ͥ����ƽ����ˮ��������12�ֵĻ�������.
�⣺(1)��ͼ��ʾ.
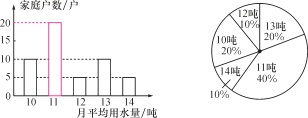
��2��11.6��11��11
(3)��¥��ֱ������300����ͥ����ƽ����ˮ��������12�ֵ�Լ��300��(20%��40%��10%)��210(��).



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ 1������ OC�ڡ�AOB���ڲ���ͼ�й��� 3���ǣ���AOB����AOC �͡�BOC����������һ���ǵĶ�������һ���Ƕ������������������ OC�ǡ�AOB�������ߣ�
��1��һ���ǵĽ�ƽ����_______����ǵ������ߣ������ǻ��ǣ���
��2����ͼ 2������MPN��60�������� PQ�Ƶ� P�� PNλ�ÿ�ʼ����ÿ�� 10�����ٶ���ʱ����ת������QPN�״ε��� 180��ʱֹͣ��ת������ת��ʱ��Ϊ t��s����
�� �� tΪ��ֵʱ������ PM�ǡ�QPN �������ߣ�
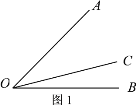
�������� PM ͬʱ�Ƶ� P��ÿ�� 5�����ٶ���ʱ����ת������ PQͬʱֹͣ��ת������������� PQ�ǡ�MPN��������ʱ t��ֵ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC���CDE�ǵ���ֱ�������Σ�ֱ�DZ�AC��CD��ͬһ��ֱ���ϣ���M��N�ֱ���б��AB��DE���е㣬��PΪAD���е㣬����AE��BD��MN��
(1)��֤����PMNΪ����ֱ�������Σ�
(2)�ֽ�ͼ���еġ�CDE���ŵ�C˳ʱ����ת��(0�㣼����90��)���õ�ͼ����AE��MP��BD�ֱ��ڵ�G��H�����ж����еĽ����Ƿ����������������֤����������������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABCD�У�AE��BC�ڵ�E���Ե�BΪ���ģ�ȡ��ת�ǵ�����ABC������BAE˳ʱ����ת���õ���BA��E��������DA��������ADC=60������ADA��=50��������DA��E���Ĵ�СΪ�� ��
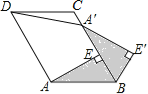
A. 130�� B. 150�� C. 160�� D. 170��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
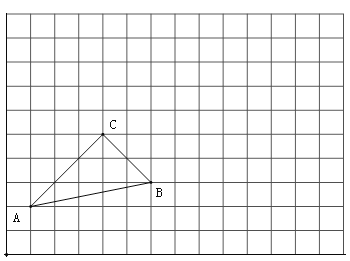
����Ŀ����ͼ����ABC�Ǹ�������Σ��������������ߵĽ��㣩�� ÿ��С�����DZ߳�Ϊ1����λ���ȵ�С�����Σ�
��1������ABC����ƽ��6����λ���ȣ�����ƽ�ƺ����A1B1C1��
��2����ƽ�ƺ����A1B1C1�Ƶ�B1˳ʱ����ת90����������ת�����A2B1C2��
��3������ABC��ֱ��BC���ۣ��������ۺ����A3BC.
��4��������ABC�ܷ�һ����ת������A2B1C2�غϣ����ܣ�����ͼ������ĸO��ʾ��ת���IJ�д����ת�ǵĴ�С�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����m+n+1��x+m��n��0��������ʵ����Ϊ�����£��Ҧ��ܦ£�
��1�����ú������µĴ���ʽ��ʾm��n��
��2����֤������1�ܦ£�
��3������P�������£�����ABC�����������˶�������ABC���������ֱ�ΪA��1��2����B��![]() ��1����C��1��1�������Ƿ���ڵ�P��ʹm+n=
��1����C��1��1�������Ƿ���ڵ�P��ʹm+n=![]() �������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� a��b��c �������϶�Ӧ�ĵ��λ�ã���ͼ��ʾ���� abc��0���� |a��b|��|b��c|��|a��c|���� (a��b)(b��c)(c��a)��0���� |a|��1��bc�������ĸ�������ȷ���У� ����
![]()
A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ�����Ű�����ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�Ϊ�˱�֤ÿ�������۳�260��Ű��̾����������ۣ�
��1����������ˮ��ÿ����ۼ۽���xԪ����ÿ����������� ��ú�x�Ĵ���ʽ��ʾ����
��2����������ˮ��Ҫ��ÿ��ӯ��300Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
��3����ÿ����ۼ۶�Ϊ����Ԫʱ��ÿ�����������ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
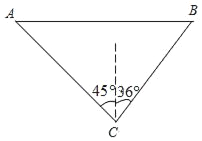
����Ŀ����ͼ��ij���ĵ�����һͤ��A����ͤ��A�����������ϵĺ�����һ����B����������ĵ��ĺ���C�����ͤ��A�ڱ�ƫ��45�������ϣ������B�ڱ�ƫ��36�������ϣ��ֲ��B��C֮��ľ������200�ף���A��B֮��ľ���
�������ȷ��1�ף������ο����ݣ�![]() ��1.414��sin36���0.588��cos36���0.809��tan36���0. 727��cot36���1.376��
��1.414��sin36���0.588��cos36���0.809��tan36���0. 727��cot36���1.376��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com