
【题目】如图,平面直角坐标系中,直线AB:y=x+b交y轴于点A(0,4),交x轴于点B.
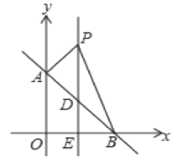
(1)求点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
(3)在(2)中②的条件下,以PB为斜边作等腰直角△PBC,求点C的坐标。
【答案】(1)(4,0);(2)①S△ABP =2n4.;②(2,6);(3)(6,4)或(0,2)
【解析】
(1)把点A的坐标代入直线解析式可求得b=4,则直线的解析式为y=-x+4,令y=0可求得x=4,故此可求得点B的坐标;
(2)①由题l垂直平分OB可知OE=BE=2,将x=2代入直线AB的解析式可求得点D的坐标,设点P的坐标为(2,n),然后依据S△APB=S△APD+S△BPD可得到△APB的面积与n的函数关系式为S△APB=2n-4;
②由S△ABP=8得到关于n的方程可求得n的值,从而得到点P的坐标;
③如图1所示,过点C作CM⊥l,垂足为M,再过点B作BN⊥CM于点N.设点C的坐标为(p,q),先证明△PCM≌△CBN,得到CM=BN,PM=CN,然后由CM=BN,PM=CN列出关于p、q的方程组可求得p、q的值;如图2所示,同理可求得点C的坐标.
(1)∵把A(0,4)代入y=x+b得b=4
∴直线AB的函数表达式为:y=x+4.
令y=0得:x+4=0,解得:x=4
∴点B的坐标为(4,0).
(2)①∵l垂直平分OB,
∴OE=BE=2.
∵将x=2代入y=x+4得:y=2+4=2.
∴点D的坐标为(2,2).
∵点P的坐标为(2,n),
∴PD=n2.
∵S△APB=S△APD+S△BPD,
∴S△ABP=![]() PDOE+
PDOE+![]() PDBE=
PDBE=![]() (n2)×2+
(n2)×2+![]() (n2)×2=2n4.
(n2)×2=2n4.
②∵S△ABP=8,
∴2n4=8,解得:n=6.
∴点P的坐标为(2,6).
(3)如图1所示:过点C作CM⊥l,垂足为M,再过点B作BN⊥CM于点N.
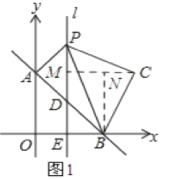
设点C(p,q).
∵△PBC为等腰直角三角形,PB为斜边,
∴PC=CB,∠PCM+∠MCB=90°.
∵CM⊥l,BN⊥CM,
∴∠PMC=∠BNC=90°,∠MPC+∠PCM=90°.
∴∠MPC=∠NCB.
在△PCM和△CBN中,
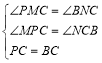 ,
,
∴△PCM≌△CBN.
∴CM=BN,PM=CN.
∴![]() ,解得
,解得![]() .
.
∴点C的坐标为(6,4).
如图2所示:过点C作CM⊥l,垂足为M,再过点B作BN⊥CM于点N.
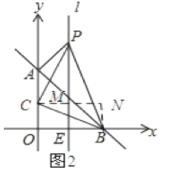
设点C(p,q).
∵△PBC为等腰直角三角形,PB为斜边,
∴PC=CB,∠PCM+∠MCB=90°.
∵CM⊥l,BN⊥CM,
∴∠PMC=∠BNC=90°,/span>∠MPC+∠PCM=90°.
∴∠MPC=∠NCB.
在△PCM和△CBN中,
 ,
,
∴△PCM≌△CBN.
∴CM=BN,PM=CN.
∴![]() ,解得
,解得![]() .
.
∴点C的坐标为(0,2).
综上所述点C的坐标为(6,4)或(0,2).


科目:初中数学 来源: 题型:
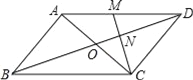
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
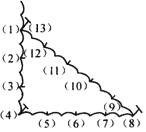
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
A. 直角三角形两个锐角互补
B. 三角形内角和等于180°
C. 如果三角形两条边长的平方和等于第三边长的平方
D. 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
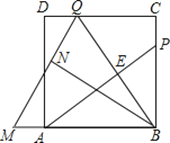
【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的形统计图和不完整的条形统计图:
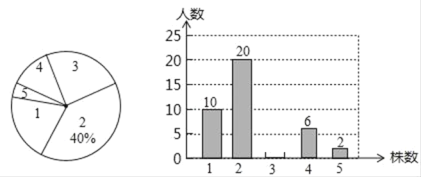
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)该班同学植树株数的中位数是 ;
(3)求该班同学平均植树的株数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
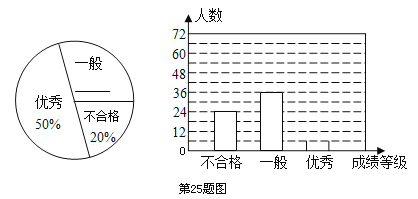
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有______人达标;
(3)若该校学生有1000人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,其中![]() ,
,![]() ,
,![]() 的圆心依次是点A,B,C.
的圆心依次是点A,B,C.
(1)求点D沿三条圆弧运动到点G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.
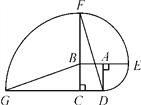
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
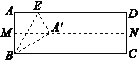

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
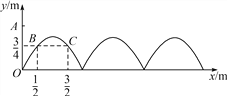
【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为![]() m,到墙边OA的距离分别为
m,到墙边OA的距离分别为![]() m,
m,![]() m.
m.
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10 m,则最多可以连续绘制几个这样的拋物线型图案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com