
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
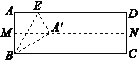

图1 图2
【答案】(1)30°;(2)见解析
【解析】
(1)由折叠的性质易得:∠ABE=∠A′BE,M是AB的中点,A′是EF的中点,∠EA′B=∠A=90°,由此可得BA′是EF的垂直平分线,从而可得BE=BF,由此可得∠A′BE=∠A′BF,从而可得∠ABE=∠A′BE=∠A′BF,这样结合∠ABC=90°即可得到∠ABE=![]() ∠ABC=30°;
∠ABC=30°;
(2)由已知条件结合折叠的性质可得:BE=B′E,BF=B′F,这样结合(1)中所得BE=BF即可得到四边形BFB′E的四边相等,由此即可得到四边形BFB′E是菱形.
(1)∵对折使AD与BC重合,折痕是MN,
∴M是AB的中点,
∴A′是EF的中点.
∵∠BA′E=∠A=90°,
∴BA′垂直平分EF,
∴BE=BF,
∴∠A′BE=∠A′BF.
由翻折的性质,知∠ABE=∠A′BE,
∴∠ABE=∠A′BE=∠A′BF,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() ×90°=30°;
×90°=30°;
(2)∵沿EA′所在的直线折叠,
点B落在AD上的点B′处,
∴BE=B′E,BF=B′F.
∵BE=BF,
∴BE=B′E=B′F=BF,
∴四边形BFB′E为菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】由一些正整数组成的数表如下(表中下一行中数的个数是上一行中数的个数的2倍):

若规定坐标号(m,n)表示第m行从左向右第n个数,则(7,4)所表示的数是_____;(5,8)与(8,5)表示的两数之积是_______;数2012对应的坐标号是_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB:y=x+b交y轴于点A(0,4),交x轴于点B.
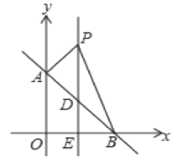
(1)求点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
(3)在(2)中②的条件下,以PB为斜边作等腰直角△PBC,求点C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A逆时针旋转80°后得到△A′B′C′(点B的对应点是点B′,点C的对应点是点C′,连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
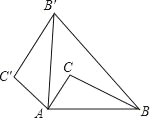
A. 82° B. 80° C. 78° D. 76°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化.
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=10,b=12时的绿化面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是中线,作
是中线,作![]() 关于
关于![]() 的轴对称图形
的轴对称图形![]() .
.
(1)直接写出![]() 和
和![]() 的位置关系;
的位置关系;
(2)连接![]() ,写出
,写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() ,
,![]() 时,在
时,在![]() 上找一点
上找一点![]() ,使得点
,使得点![]() 到点
到点![]() 与到点
与到点![]() 的距离之和最下小,求
的距离之和最下小,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在完成第10章的学习后,遇到了一些问题,请你帮助他.
(1)图1中,当![]() ,试说明
,试说明![]() .
.
(2)图2中,若![]() ,则
,则![]() 吗?请说明理由.
吗?请说明理由.
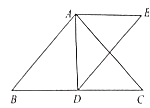
(3)图3中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ______(直接写出结果,用含x,y,z的式子表示)
______(直接写出结果,用含x,y,z的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com