
【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化.
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=10,b=12时的绿化面积.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
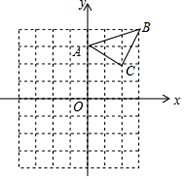
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的形统计图和不完整的条形统计图:
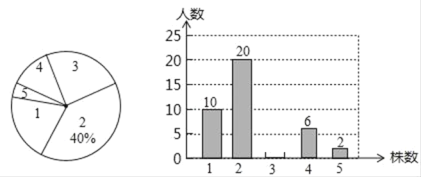
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)该班同学植树株数的中位数是 ;
(3)求该班同学平均植树的株数.
查看答案和解析>>
科目:初中数学 来源: 题型:
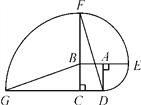
【题目】如图,四边形ABCD是边长为1的正方形,其中![]() ,
,![]() ,
,![]() 的圆心依次是点A,B,C.
的圆心依次是点A,B,C.
(1)求点D沿三条圆弧运动到点G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
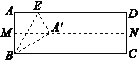

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月12日,安庆“筑梦号”自动驾驶公开试乘体验正式启动,让安庆成为全国率先开通自动驾驶的城市,智能、绿色出行的时代即将到来.普通燃油车从A地到B地,所需油费108元,而自动驾驶的纯电动车所需电费27元,已知每行驶l千米,普通燃油汽车所需的油费比自动的纯电动汽车所需的电费多0.54元,求自动驾驶的纯电动汽车每行驶1千米所需的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点P在AD上,AB=![]() ,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图).
,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图).

(1)当点E与点B重合时,点F恰好与点C重合(如图),则PC的长为 ;
(2)将直角尺从如图中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径(线段)长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com